

Optimisation / fonction
Mathematiques > sujets expliqués - 06/12/2017 - correction
    
|
 | optimisation / fonction revenir au plan | docs | ||
| Je souhaite recevoir par mail lire |  | |||
 | Bonjour, je vais regarder votr lire | |||
| Non. je suis bloqué dès la p lire | ||||
 | Bonjour, je ne peux donner un lire | |||
Bonjour, je ne peux donner un corrigé directement mais vous fournir des pistes afin de résoudre votre exercice. Il faut que vous cherchiez par vous même.
Pour la partie 1:
1a) On rappele que la formule d'un volume d'une boite est : Aire de la base x hauteur. Si vous remplacez x par 2 vous trouverez aisément les longueurs de chacun des côtés.
2) de même pour cette question, on applique la même formule en faisant attention à la valeur x. la hauteur sera donc cette valeur et un des côtés de la base 25-2x. Je vous laisse terminer.
3) Le but est de faire une boite à partir d'un carré en acier de côt?éx, réfléchissez à ce qui se passerait si vous preniez telle ou telle valeurs ( par exemple puis je prendre 25cm, non car je ne pourrais pas faire de boîte sans découpage) ...
A partir des valeurs impossibles vous pouvez en déduire l'ensemble de définition aisément.
4) 1)Si vous ne l'avez pas trouvée, la fonction v(x)=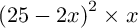
Avec votre calculatrice vous pourrez obtenir le tableau de valeurs et donc compléter.
2) A l'aide du tableau de valeur on vous demande de représenter graphiquement la fonction.
3) On vous demande de rechercher sur la représentation à quel(s) endroit la fonction v?rifie f(x)=500 d'une part et f(x)=1000 d'autre part.
Partie 2:
1) Comment trouve t-on un maximum sur une courbe ? en regardant le point le plus haut. De la même manière comment trouve t-on un minimum sur une courbe ? en regardant le point le plus bas.
2) Toujours à partir de votre calculatrice.
3) Aidez vous de sa représentation graphique et de ses extremums.
Pour la partie 1:
1a) On rappele que la formule d'un volume d'une boite est : Aire de la base x hauteur. Si vous remplacez x par 2 vous trouverez aisément les longueurs de chacun des côtés.
2) de même pour cette question, on applique la même formule en faisant attention à la valeur x. la hauteur sera donc cette valeur et un des côtés de la base 25-2x. Je vous laisse terminer.
3) Le but est de faire une boite à partir d'un carré en acier de côt?éx, réfléchissez à ce qui se passerait si vous preniez telle ou telle valeurs ( par exemple puis je prendre 25cm, non car je ne pourrais pas faire de boîte sans découpage) ...
A partir des valeurs impossibles vous pouvez en déduire l'ensemble de définition aisément.
4) 1)Si vous ne l'avez pas trouvée, la fonction v(x)=
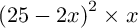
Avec votre calculatrice vous pourrez obtenir le tableau de valeurs et donc compléter.
2) A l'aide du tableau de valeur on vous demande de représenter graphiquement la fonction.
3) On vous demande de rechercher sur la représentation à quel(s) endroit la fonction v?rifie f(x)=500 d'une part et f(x)=1000 d'autre part.
Partie 2:
1) Comment trouve t-on un maximum sur une courbe ? en regardant le point le plus haut. De la même manière comment trouve t-on un minimum sur une courbe ? en regardant le point le plus bas.
2) Toujours à partir de votre calculatrice.
3) Aidez vous de sa représentation graphique et de ses extremums.
| Documents attachés : | aucun document joint. |
Matières disponibles
sciences
. chimie
. mathématiques
. physique
. biologie
langues vivantes
. anglais
. espagnol
. allemand
. italien
lettres
. français
. lettres
sciences humaines
. philosophie
. histoire
. SES-éco
. droit
. culture générale
. géographie
Niveaux scolaires
. Collège
. Lycée
. Fac (DEUG)
. Classes préparatoires - CPGE
. BTS
. DUT
. Fac (> DEUG)
. Ecoles (> BAC+2)
parents d'élèves : nos conseils
Qu'est-ce que Cyberprofs.com ?
Derniers devoirs traités