
Exercice 42 page 151 des annales bac tes 2009
Mathematiques > sujets expliqués - 26/03/2009 - correction
    
|
 | exercice 42 page 151 des annal revenir au plan | docs | ||
| J'ai fait l'exercice 43 mais j lire | ||||
 | Bonjour, Scannez nous l'én lire | |||
| soit f la fonction déf sur l' lire | ||||
 | 1) pour déterminer la limite lire | |||
1) pour déterminer la limite de f en 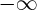 il suffit de se servir des limites usuelles.
il suffit de se servir des limites usuelles.
On sait que :
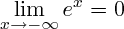
D'où :
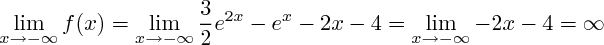
Pour montrer que g(x) s'annule en ln(2/3), il suffit de calculer g(ln(2/3)) et de se souvenir que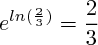 .
.
Pour étudier le signe de g il faut remarquer que g est déjà factorisée. Si ce n'était pas le cas où si la fonction g était plus compliquée on peut suivre les étapes suivantes (c'est lourd mais marche tout le temps) :
- calculer g'
- étudier le signe de g'
- calculer les limites de g aux bornes de son intervalle de définition
- en déduire le signe de g
Ici c'est plus simple :
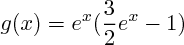 or on sait que
or on sait que 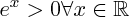 ainsi le signe de g ne dépend que de
ainsi le signe de g ne dépend que de 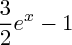 qui est négatif de
qui est négatif de 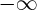 à
à 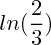 et positif ensuite.
et positif ensuite.
On a le signe de g.
Pour montrer que f(x)-(-2x-4)=g(x) il suffit de calculer f(x)-(-2x-4) et mettre e^x en facteur.
b) Pour montrer que la droite d'équation y=-2x-4 est asymptote à (c) en -infini, il faut montrer que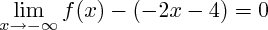 ce qui revient à calculer la limite de g et est un calcul similaire à celui de la première limite.
ce qui revient à calculer la limite de g et est un calcul similaire à celui de la première limite.
4) Pour factoriser f' deux solutions sont possibles :
On connait le résultat, on peut donc écrire
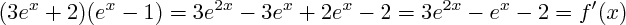
Ou sinon chercher les racines du polynôme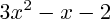 le factoriser et en déduire le résultat sur f'.
le factoriser et en déduire le résultat sur f'.
Pour le signe de f' maintenant qu'elle est factorisée il s'agit d'un raisonnement similaire à la question 1)
Bon courage !
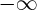 il suffit de se servir des limites usuelles.
il suffit de se servir des limites usuelles.On sait que :
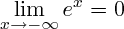
D'où :
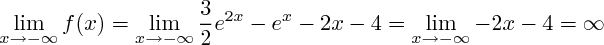
Pour montrer que g(x) s'annule en ln(2/3), il suffit de calculer g(ln(2/3)) et de se souvenir que
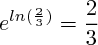 .
.Pour étudier le signe de g il faut remarquer que g est déjà factorisée. Si ce n'était pas le cas où si la fonction g était plus compliquée on peut suivre les étapes suivantes (c'est lourd mais marche tout le temps) :
- calculer g'
- étudier le signe de g'
- calculer les limites de g aux bornes de son intervalle de définition
- en déduire le signe de g
Ici c'est plus simple :
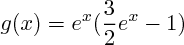 or on sait que
or on sait que 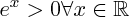 ainsi le signe de g ne dépend que de
ainsi le signe de g ne dépend que de 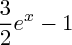 qui est négatif de
qui est négatif de 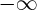 à
à 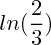 et positif ensuite.
et positif ensuite.On a le signe de g.
Pour montrer que f(x)-(-2x-4)=g(x) il suffit de calculer f(x)-(-2x-4) et mettre e^x en facteur.
b) Pour montrer que la droite d'équation y=-2x-4 est asymptote à (c) en -infini, il faut montrer que
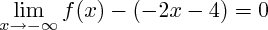 ce qui revient à calculer la limite de g et est un calcul similaire à celui de la première limite.
ce qui revient à calculer la limite de g et est un calcul similaire à celui de la première limite.4) Pour factoriser f' deux solutions sont possibles :
On connait le résultat, on peut donc écrire
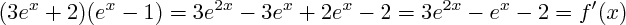
Ou sinon chercher les racines du polynôme
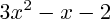 le factoriser et en déduire le résultat sur f'.
le factoriser et en déduire le résultat sur f'.Pour le signe de f' maintenant qu'elle est factorisée il s'agit d'un raisonnement similaire à la question 1)
Bon courage !
| Documents attachés : | aucun document joint. |

