Pour E :
Il y a une CNS triviale que doit v?rifier (x,y,z,t) pour qu'il soit dans E .
Pour D :
Si on d?signe par (x,y,z,t) les coordonn?es d'un ?l?ment de
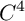
, dans sa base canonique (e1,e2,e3,e4) on a :
(x,y,z,t)

D SSI il existe (u , v)

C? tel que (x,y,z,t) = u .(1 , 0 , -i , i - 1) + v.(i , 1 - i , 1 , 0) .
En "?liminant u et v " tu trouves 2 relations entre x , y , z , t de la forme ax + by + cz + dt = 0 et a'x + b'y + c'z + d't = 0 o? (a,b,,c,d) et (a',b',,c',d') sont 2 ?l?ments lin?airement ind?pendants de sup]4[/sup] .
Si tu montres la r?ciproque , c?d que si (x,y,z,t) v?rifie ax + by + cz + dt = 0 et a'x + b'y + c'z + d't = 0 alors il est combinaison lin?aire de (1 , 0 , -i , i - 1) et (i , 1 - i , 1 , 0) , vous pourrez dire que ax + by + cz + dt = 0 , a'x + b'y + c'z + d't = 0 est un syst?me d'?quations de D .





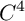 , dans sa base canonique (e1,e2,e3,e4) on a :
, dans sa base canonique (e1,e2,e3,e4) on a :  D SSI il existe (u , v)
D SSI il existe (u , v)  C? tel que (x,y,z,t) = u .(1 , 0 , -i , i - 1) + v.(i , 1 - i , 1 , 0) .
C? tel que (x,y,z,t) = u .(1 , 0 , -i , i - 1) + v.(i , 1 - i , 1 , 0) .