
Coorection exercice
Mathematiques > sujets expliqués - 10/02/2010 - correction
    
|
 | Coorection Exercice revenir au plan | docs | ||
| Bonjour pouvez vous corriger m lire | ||||
 | Bonjour, Alors on va commen lire | |||
Bonjour,
Alors on va commencer par répondre à la première partie, à savoir la dérivée de la fonction. Tu as dû voir en cours certaines dérivées usuelles de fonctions classiques ainsi que la dérivée de fonctions composées.
Voyons à quoi nous avons à faire :
- La fonction B est une somme de trois fonctions:
- A(x) = -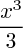
- F(x) = 49x
- G(x) = -100
Afin de dériver la somme des trois fonctions, tu dois faire la somme des dérivées de chacune des fonctions (cf. ton cours)
La fonction A est du type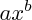
ton cours te dit que la dérivée d'une telle fonction est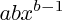
Pour toi, ce sera alors A'(x) =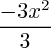 soit
soit 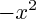
F'(x) = 49 (taux d'accroissement de la fonction affine F)
Et enfin G'(x) = 0 car G est constante.
Si tu sommes tu obtiens : B'(x) =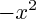 +49.
+49.
Suite du problème, tu veux annuler cette fonction, on veut alors résoudre l'équation suivante :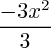 + 49 = 0.
+ 49 = 0.
En passant les x du même côté du signe "=" on obtient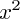 = 49.
= 49.
Tu obtiens alors simplement x = 7 ou x = -7.
J'espère que tu as bien tout compris.
Alors on va commencer par répondre à la première partie, à savoir la dérivée de la fonction. Tu as dû voir en cours certaines dérivées usuelles de fonctions classiques ainsi que la dérivée de fonctions composées.
Voyons à quoi nous avons à faire :
- La fonction B est une somme de trois fonctions:
- A(x) = -
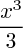
- F(x) = 49x
- G(x) = -100
Afin de dériver la somme des trois fonctions, tu dois faire la somme des dérivées de chacune des fonctions (cf. ton cours)
La fonction A est du type
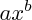
ton cours te dit que la dérivée d'une telle fonction est
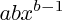
Pour toi, ce sera alors A'(x) =
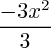 soit
soit 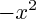
F'(x) = 49 (taux d'accroissement de la fonction affine F)
Et enfin G'(x) = 0 car G est constante.
Si tu sommes tu obtiens : B'(x) =
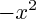 +49.
+49.Suite du problème, tu veux annuler cette fonction, on veut alors résoudre l'équation suivante :
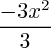 + 49 = 0.
+ 49 = 0.En passant les x du même côté du signe "=" on obtient
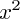 = 49.
= 49.Tu obtiens alors simplement x = 7 ou x = -7.
J'espère que tu as bien tout compris.
| Documents attachés : | aucun document joint. |

