
équations
Mathematiques > sujets expliqués - 12/11/2008 - correction
    
|
Pour la première équation, il ne fallait pas développer ! Lorsqu'on a (2x+5)²=7 il suffit de dire que 2x+5=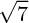 ou
ou 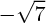 et donc
et donc 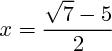 ou
ou 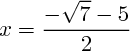
Deuxième équation : pourquoi tout multiplier par (x+1) ??? Il suffit de tout réduire au même dénominateur, ici 6, ce qui donne :
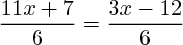
et après simplification par 6, la résolution est simple. On trouve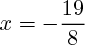
Troisième équation : le calcul est juste, et lorsque l'on arrive à [Formule incorrecte ou erreur de parsing. Erreur 6 ] on conclut en utilisant la racine carrée :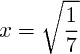 ou bien
ou bien 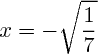 .
.
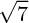 ou
ou 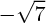 et donc
et donc 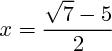 ou
ou 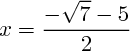
Deuxième équation : pourquoi tout multiplier par (x+1) ??? Il suffit de tout réduire au même dénominateur, ici 6, ce qui donne :
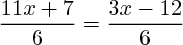
et après simplification par 6, la résolution est simple. On trouve
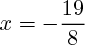
Troisième équation : le calcul est juste, et lorsque l'on arrive à [Formule incorrecte ou erreur de parsing. Erreur 6 ] on conclut en utilisant la racine carrée :
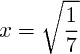 ou bien
ou bien 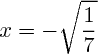 .
. | Documents attachés : | aucun document joint. |



