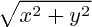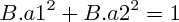Bonjour,
Pour commencer, on prend le point O1 comme centre du repère, avec comme axes (x,y,z). x est l'axe horizontal dirigé vers la droite, y l'axe vertical dirigé vers le haut et z l'axe dirigé vers nous mais nous n'en aurons pas besoin.
1) Il s'agit dans cette question de positionner les points A, B, C, D et O2 par rapport au point d'origine O1.
J'ai fait un schéma en PJ pour aider à visualiser les angles et les distances avec les données que l'on a. Je vais t'écrire le détail pour un des points, et ça devrait t'aider à comprendre la démarche pour les autres points.
Par exemple pour le point B :
On projette O1B sur l'axe x horizontal, et on cherche la distance correspondante. En positionnant l'angle alpha de 30° aux bons endroits sur le schéma on trouve que cette distance vaut r.sinus(30) avec les formules trigonométriques. La projection de B se trouve à droite de O1 donc dans le sens de l'axe x : la valeur est donc positive.
On projette O1B sur l'axe vertical : de même on trouve que cette valeur vaut r.cosinus(30). B se retrouve en dessous de O1 donc en sens inverse par rapport à la direction de l'axe y : la valeur est donc négative.
On reste tout le temps dans le plan de la feuille donc la valeur sur l'axe z vaut toujours 0.
Alors les coordonnées de B sont : (r.sin(30) ; -r.cos(30) ; 0).
Tu peux faire de même pour les autres points.
2) On te demande les coordonnées de vecteurs. Pour un vecteur AB les coordonnées sont : les coordonnées de B - les coordonnées de A dans le repère.
Les vecteurs demandés ici ont tous pour origine O1, or O1 est le centre du repère donc les coordonnées de O1 sont toutes nulles.
Alors les coordonnées des vecteurs O1A, O1B, O1C, O1D, O1O2 sont les mêmes que celles des points A, B, C, D, O2 (réponse à la question 1).
3) On essaie de trouver les coordonnées de O1D à partir des autres vecteurs. On va décomposer le vecteur en somme de vecteurs pour cela. Par exemple de façon générale : AB = AC + CB. On va faire de même ici en essayant de retrouver les vecteurs restants.
4) Le vecteur u est unitaire donc sa norme doit valoir 1. Pour un vecteur AB de coordonnées (x, y) la norme s'exprime :
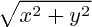
On sait aussi que u est sur la droite dirigée par O1O2 donc u est parallèle (colinéaire) à O1O2. Ses coordonnées sont donc proportionnelles à celles de O1O2. Notons a1 et a2 les coordonnées de O1O2 que tu auras trouvé en question 2.
Alors si on prend un facteur de proportionnalité B, les coordonnées de u sont donc (B.a1 ; B.a2). Et on sait que :
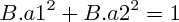
Il ne te reste plus qu'à trouver B comme solution de cette équation, et tu trouveras les coordonnées de u (B.a1, B.a2).
5) Il te suffit de faire le produit scalaire des deux vecteurs et de montrer qu'il est nul.
6) Le produit scalaire de deux vecteurs peut s'exprimer de deux façons. Avec les coordonnées (pour répondre à la question 5) ou comme ça : x.y = norme de x . norme y . cosinus(alpha) avec alpha l'angle entre les deux vecteurs. Tu connais les coordonnées de O1O2 et de O1D donc tu peux calculer le produit scalaire des deux façons. ça te donner une équation dont l'inconnue sera cosinus(alpha) ce qui t'amènera à la valeur d'alpha.
7) Cela correspond à la valeur de la norme du vecteur AD.
8) Formule du produit vectoriel.
9) Tu refais le schéma que je t'ai mis en pièce jointe mais dans le repère (e1, e2) cette fois ci en plaçant bien toutes tes données (distances et angles) et tu reprends exactement le même raisonnement.
10) A toi de conclure à la fin des calculs selon les difficultés rencontrées avec chaque méthode :-)