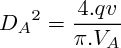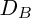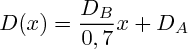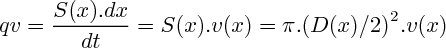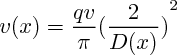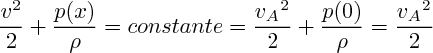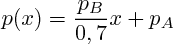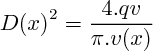Etude d'une tuyère :
1) a)En A, la surface de la tuyère vaut :
Le débit volumique vaut
donc
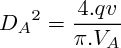
De même pour
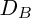
b) On suppose que le diamètre varie linéairement avec x. On prend x(A)=0.
On a donc
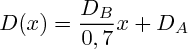
c) On a toujours
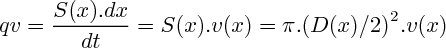
donc
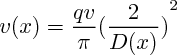
d) On utilise le théorème de Bernoulli, en prenant z=0 :
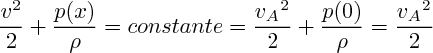
d'où p(x)
2)La loi de Bernoulli nous donne
[Formule incorrecte ou erreur de parsing. Erreur 6 ]
On trouve alors la loi linéaire donnant la pression :
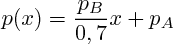
On a donc
[Formule incorrecte ou erreur de parsing. Erreur 6 ]
puis
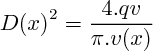Installation de pompage :
D'après la formule de Darcy, les pertes de charge valent :
[Formule incorrecte ou erreur de parsing. Erreur 6 ]
Par définition du coefficient de résistance hydraulique, [Formule incorrecte ou erreur de parsing. Erreur 6 ]
