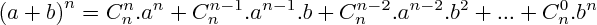DÉFINITIONS
Une
combinaison est un ensemble non orienté d'éléments, qui ne peuvent pas se répéter.
Un
arrangement est un ensemble orienté d'éléments, qui ne peuvent pas se répéter.
Un
n-uplet est un ensemble orienté d'éléments qui peuvent se répéter.
On note
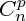
le nombre de combinaisons distinctes de p éléments pris parmi
n, et on note
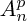
le nombre d'arrangements distincts de
p éléments pris parmi n.
PROPRIÉTÉS
Il existe
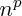
p-uplets d'éléments pris parmi n, distincts.
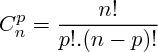
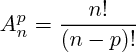
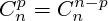
Le binôme de Newton
Dans le développement d'une expression du type :
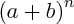
, les coefficients des différents termes en a et b sont les coefficients du " triangle de Pascal " :
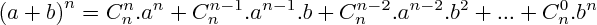
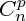 le nombre de combinaisons distinctes de p éléments pris parmi n, et on note
le nombre de combinaisons distinctes de p éléments pris parmi n, et on note 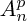
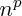 p-uplets d'éléments pris parmi n, distincts.
p-uplets d'éléments pris parmi n, distincts. 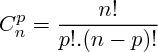
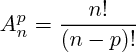
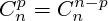
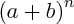 , les coefficients des différents termes en a et b sont les coefficients du " triangle de Pascal " :
, les coefficients des différents termes en a et b sont les coefficients du " triangle de Pascal " :