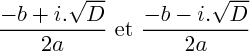DÉFINITION
On définit un nombre, noté i, tel que :
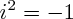
ce nombre n'est donc pas un réel. Il appartient à l'ensemble des nombres complexes, qui inclut aussi l'ensemble des réels ; les règles de calcul usuelles dans
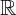
sont aussi valables dans

(l'ensemble des complexes) : les opérations d'addition, de multiplication, ... sont généralisées à

.
Tout nombre complexe peut s'écrire comme une somme d'un réel, et d'un imaginaire pur (i.e. : un multiple de
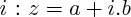
) où a et b sont des
coefficients réels
On appelle a " partie réelle " de z, et b, " partie imaginaire " de
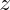
.
On peut représenter un complexe
z=a+i.b sur un plan muni d'un repère :
(a,b), appelée " affixe de z " sont les coordonnées d'un point M qui représente le complexe z.
On appelle " complexe conjugué " de
z le complexe qui a la même partie réelle que
z, et une partie imaginaire opposée à celle de z.
MODULE D'UN COMPLEXE
c'est la distance entre le point repésentatif M et l'origine de ce repère orthonormé ; le module de
z=a+i.b vaut donc :
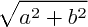
Pour tout complexe non nul, il existe un unique réel positif r, et un unique réel thêta compris entre 0 et
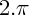
, tels que :
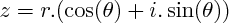
(
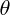
est une mesure de l'angle orienté entre le vecteur directeur de l'axe des réels et OM, et r est le module de z)
Pour des raisons qui ne sont pas au programme de terminale, on note également ce complexe :
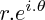
, et les règles de calcul sur les exponentielles complexes sont les mêmes que sur les exponentielles réelles.
PROBLÈMES DU SECONDE DEGRÉ (ax2+bx+c=0, avec a, b et c réels) dans l'ensemble complexe
Les équations du second degré à
discriminant négatif admettent des solutions dans l'ensemble des complexes dans la démonstration de l'utilité du discriminant, en première, on montrait que ces équations n'admettaient pas de racine réelle, parce qu'il aurait fallu que
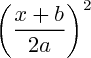
soit égal à
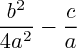
, qui est négatif quand le discriminant est négatif).
Si on admet que
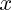
peut être complexe sans être nécessairement réel : l'équation admet deux racines, qui sont conjuguées :
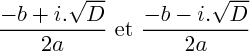
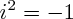 ce nombre n'est donc pas un réel. Il appartient à l'ensemble des nombres complexes, qui inclut aussi l'ensemble des réels ; les règles de calcul usuelles dans
ce nombre n'est donc pas un réel. Il appartient à l'ensemble des nombres complexes, qui inclut aussi l'ensemble des réels ; les règles de calcul usuelles dans 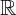 sont aussi valables dans
sont aussi valables dans  (l'ensemble des complexes) : les opérations d'addition, de multiplication, ... sont généralisées à
(l'ensemble des complexes) : les opérations d'addition, de multiplication, ... sont généralisées à  .
.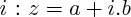 ) où a et b sont des coefficients réels
) où a et b sont des coefficients réels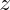 .
.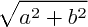
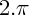 , tels que :
, tels que :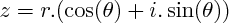
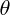 est une mesure de l'angle orienté entre le vecteur directeur de l'axe des réels et OM, et r est le module de z)
est une mesure de l'angle orienté entre le vecteur directeur de l'axe des réels et OM, et r est le module de z) 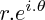 , et les règles de calcul sur les exponentielles complexes sont les mêmes que sur les exponentielles réelles.
, et les règles de calcul sur les exponentielles complexes sont les mêmes que sur les exponentielles réelles.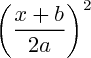 soit égal à
soit égal à 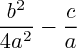 , qui est négatif quand le discriminant est négatif).
, qui est négatif quand le discriminant est négatif).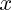 peut être complexe sans être nécessairement réel : l'équation admet deux racines, qui sont conjuguées :
peut être complexe sans être nécessairement réel : l'équation admet deux racines, qui sont conjuguées :