DÉFINITIONS
On appelle "
primitive de f " sur un certain intervalle, une fonction dont la dérivée, sur cet intervalle, est égale à
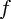
(qui doit être continue sur cet intervalle).
Remarque : une fonction
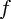
, continue sur un intervalle
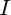
, a une infinité de primitives sur cet intervalle ; elles sont égales les unes aux autres, à une constante additive près (puisque, quelle que soit cette constante, la dérivation la fera disparaître).
On appelle "
intégrale de f " sur l'intervalle
![$ [a;b] $ $ [a;b] $](/latexrender/pictures/xbd30a443acff524593a3bd35c13da844.png.pagespeed.ic.LpZq1SYSuq.png)
(où
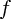
est continue) la valeur :

où
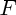
est une primitive de
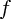
(n'importe laquelle : puisqu'elles ne diffèrent que par une constante additive, et que cette constante disparaît quand on fait la soustraction

).
PROPRIÉTÉ
L'intégrale de
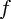
sur
![$ [a;b] $ $ [a;b] $](/latexrender/pictures/xbd30a443acff524593a3bd35c13da844.png.pagespeed.ic.LpZq1SYSuq.png)
est égale à la surface comprise entre l'axe des abscisses, et la courbe représentative de
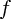
, dans un repère orthonormé.
MÉTHODES DE CALCUL DES INTÉGRALES
Il faut se ramener à des intégrales de fonctions dont on connaît des primitives (par exemple, on connaît des primitives de
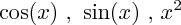
, ...) ; si aucune fonction facilement intégrable n'apparaît, on la fait apparaître en utilisant la formule d'intégration par parties.
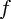 (qui doit être continue sur cet intervalle).
(qui doit être continue sur cet intervalle).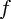 , continue sur un intervalle
, continue sur un intervalle 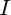 , a une infinité de primitives sur cet intervalle ; elles sont égales les unes aux autres, à une constante additive près (puisque, quelle que soit cette constante, la dérivation la fera disparaître).
, a une infinité de primitives sur cet intervalle ; elles sont égales les unes aux autres, à une constante additive près (puisque, quelle que soit cette constante, la dérivation la fera disparaître).![$ [a;b] $ $ [a;b] $](/latexrender/pictures/xbd30a443acff524593a3bd35c13da844.png.pagespeed.ic.LpZq1SYSuq.png) (où
(où 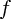 est continue) la valeur :
est continue) la valeur : où
où 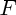 est une primitive de
est une primitive de 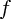 (n'importe laquelle : puisqu'elles ne diffèrent que par une constante additive, et que cette constante disparaît quand on fait la soustraction
(n'importe laquelle : puisqu'elles ne diffèrent que par une constante additive, et que cette constante disparaît quand on fait la soustraction  ).
).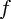 sur
sur ![$ [a;b] $ $ [a;b] $](/latexrender/pictures/xbd30a443acff524593a3bd35c13da844.png.pagespeed.ic.LpZq1SYSuq.png) est égale à la surface comprise entre l'axe des abscisses, et la courbe représentative de
est égale à la surface comprise entre l'axe des abscisses, et la courbe représentative de 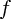 , dans un repère orthonormé.
, dans un repère orthonormé.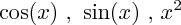 , ...) ; si aucune fonction facilement intégrable n'apparaît, on la fait apparaître en utilisant la formule d'intégration par parties.
, ...) ; si aucune fonction facilement intégrable n'apparaît, on la fait apparaître en utilisant la formule d'intégration par parties.