DÉFINITION
Ce sont des équations qui font intervenir une fonction (notée
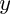
) et sa dérivée première (pour le
premier ordre), ou ses deux premières dérivées (pour le
second ordre). Ces équations s'appliquent sur des intervalles, où les fonctions solutions (et leurs dérivées intervenant dans l'équation) doivent être définies.
Exemples
Equation différentielle du premier ordre :
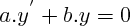
(a et b sont les " coefficients constants " : ce ne sont pas des fonctions de
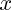
)
E
quation différentielle du second ordre :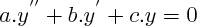
(a, b et c constants)
Elles sont dites " sans second membre ", parce que le terme à droite de l'égalité est nul.
RÉSOLUTION
Résoudre une équation différentielle signifie : trouver l'ensemble des fonctions y vérifiant l'équation, sur l'intervalle considéré.
Théorème
Les solutions d'une équation différentielle du premier ordre à coefficients constants sans second membre
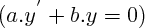
sont de la forme :
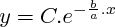
avec C : constante
Le nombre et la forme des solutions d'une équation différentielle du second ordre à coefficients constants sans second membre
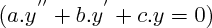
dépendent du signe du discriminant de l' "
équation caractéristique " de l'équation différentielle ; cette équation caractéristique est :
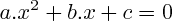
.
Si le discriminant est nul, les solutions sont de la forme :
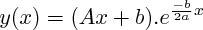
(A et B : constantes)
Si le discriminant est strictement positif, les solutions sont de la forme :
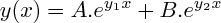
Avec : A, B : constantes,
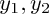
: les deux racines de l'équation caractéristique
Si le discriminant est strictement négatif, l'équation caractéristique admet alors =deux racines complexes conjuguées :
k+i.
l et
k-i.
l, avec
k et
l réels : les solutions sont de la forme : y(x)=e
k.x(A.cos(
l.x) + B.sin(
l.x))
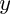 ) et sa dérivée première (pour le premier ordre), ou ses deux premières dérivées (pour le second ordre). Ces équations s'appliquent sur des intervalles, où les fonctions solutions (et leurs dérivées intervenant dans l'équation) doivent être définies.
) et sa dérivée première (pour le premier ordre), ou ses deux premières dérivées (pour le second ordre). Ces équations s'appliquent sur des intervalles, où les fonctions solutions (et leurs dérivées intervenant dans l'équation) doivent être définies.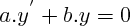
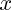 )
)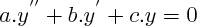 (a, b et c constants)
(a, b et c constants)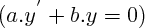 sont de la forme :
sont de la forme : 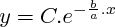 avec C : constante
avec C : constante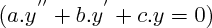 dépendent du signe du discriminant de l' " équation caractéristique " de l'équation différentielle ; cette équation caractéristique est :
dépendent du signe du discriminant de l' " équation caractéristique " de l'équation différentielle ; cette équation caractéristique est :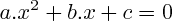 .
.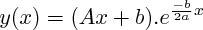
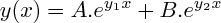
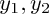 : les deux racines de l'équation caractéristique
: les deux racines de l'équation caractéristique