LIMITES
Les fonctions
exponentielle (qui associe au réel

la valeur
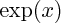
,
logarithme (qui associe au réel
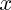
la valeur
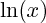
) et
puissance (qui associe au réel
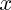
la valeur
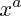
, avec
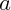
réel) tendent vers des limites aux bornes de leurs intervalles de définition ;
on peut se demander quelles seront les limites (si elles existent) des fonctions produits
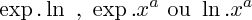
THÉORÈMES
Ces fonctions produits admettent des limites aux bornes de leurs intervalles de définition.
Dans un produit
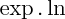
ou
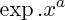
, s'il y a indétermination, c'est l'exponentielle qui impose sa limite (exemple :
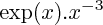
tend vers
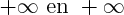
).
Dans un produit
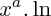
, s'il y a indétermination, c'est la fonction puissance qui impose sa limite.
 la valeur
la valeur 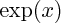 , logarithme (qui associe au réel
, logarithme (qui associe au réel 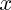 la valeur
la valeur 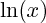 ) et puissance (qui associe au réel
) et puissance (qui associe au réel 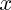 la valeur
la valeur 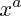 , avec
, avec 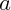 réel) tendent vers des limites aux bornes de leurs intervalles de définition ;
réel) tendent vers des limites aux bornes de leurs intervalles de définition ;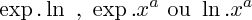
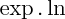 ou
ou 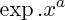 , s'il y a indétermination, c'est l'exponentielle qui impose sa limite (exemple :
, s'il y a indétermination, c'est l'exponentielle qui impose sa limite (exemple : 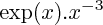 tend vers
tend vers 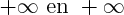 ).
).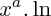 , s'il y a indétermination, c'est la fonction puissance qui impose sa limite.
, s'il y a indétermination, c'est la fonction puissance qui impose sa limite.