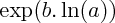FONCTION LOGARITHME
On définit la fonction "
logarithme népérien " comme la primitive, sur l'intervalle
![$ ]0;+ \infty [ $ $ ]0;+ \infty [ $](/latexrender/pictures/x96d8a40ef3da5c1015080eab65e7cd27.png.pagespeed.ic.59MEcVYPZW.png)
de la fonction inverse, qui s'annule en 1.
Notation le logarithme népérien de x se note :
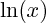
.
Propriétés du logarithme

Limites de
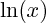
:
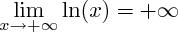
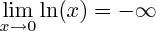
Comme

est strictement positive sur l'intervalle
![$ ]0;+ \infty[ $ $ ]0;+ \infty[ $](/latexrender/pictures/520fc306dfd34fd090af2287ec720226.png)
la fonction logarithme est strictement croissante sur son intervalle de définition.
FONCTION EXPONENTIELLE
On définit la fonction exponentielle comme la
fonction réciproque de

:
Pour tout réel
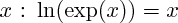
Pour tout
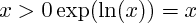
PROPRIÉTÉS DE L'EXPONENTIELLE
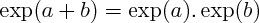
Cette propriété rappelle celle des
puissances entières des nombres réels : on va donc utiliser la notation :
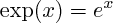
(avec e : le réel tel que
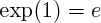
; c'est donc le réel tel que :
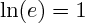
On peut alors généraliser la notion de " puissance d'un réel " aux nombres réels, et plus seulement aux entiers : si a et b sont deux réels,
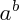
sera égal à :
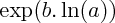
on peut vérifier que les puissances réelles de nombres réels vérifient les propriétés des puissances entières des nombres réels.
![$ ]0;+ \infty [ $ $ ]0;+ \infty [ $](/latexrender/pictures/x96d8a40ef3da5c1015080eab65e7cd27.png.pagespeed.ic.59MEcVYPZW.png) de la fonction inverse, qui s'annule en 1.
de la fonction inverse, qui s'annule en 1.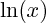 .
. 
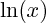 :
: 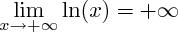
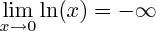
 est strictement positive sur l'intervalle
est strictement positive sur l'intervalle ![$ ]0;+ \infty[ $ $ ]0;+ \infty[ $](/latexrender/pictures/520fc306dfd34fd090af2287ec720226.png) la fonction logarithme est strictement croissante sur son intervalle de définition.
la fonction logarithme est strictement croissante sur son intervalle de définition. :
: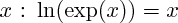
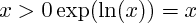
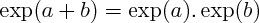
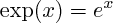 (avec e : le réel tel que
(avec e : le réel tel que 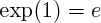 ; c'est donc le réel tel que :
; c'est donc le réel tel que : 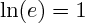
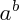 sera égal à :
sera égal à :