DÉFINITION
Le produit vectoriel de deux vecteurs
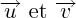
est un vecteur noté

, tel que :
1. La norme du produit vectoriel
est égale au produit des normes de
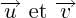
multiplié par le
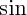
de l'angle qu'ils font (
angle non orienté : il faut que ce
sinus soit positif, pour que la norme du produit vectoriel soit positive)
2. Le produit vectoriel est perpendiculaire à chacun des deux vecteurs
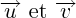
3. Le sens du produit vectoriel
est tel que le triède (
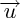
,
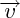
,
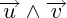
) est direct.
Analytiquement
Dans un repère orthonormé, si les coordonnées de
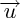
et
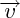
sont respectivement : (
x,y,z) et (
x',y',z'), les coordonnées
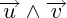
sont : (
yz'-zy',zx'-xz',xy'-yx').
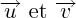 est un vecteur noté
est un vecteur noté  , tel que :
, tel que :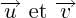 multiplié par le
multiplié par le 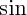 de l'angle qu'ils font (angle non orienté : il faut que ce sinus soit positif, pour que la norme du produit vectoriel soit positive)
de l'angle qu'ils font (angle non orienté : il faut que ce sinus soit positif, pour que la norme du produit vectoriel soit positive)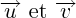
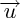 ,
, 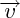 ,
, 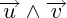 ) est direct.
) est direct.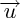 et
et 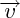 sont respectivement : (x,y,z) et (x',y',z'), les coordonnées
sont respectivement : (x,y,z) et (x',y',z'), les coordonnées 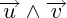 sont : (yz'-zy',zx'-xz',xy'-yx').
sont : (yz'-zy',zx'-xz',xy'-yx').