PRINCIPE
C'est un raisonnement utile lorsqu'on veut démontrer qu'une
propriété, dépendant d'un entier n, est valable quel que soit
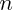
. La propriété sera notée
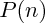
.
Exemple : la propriété
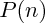
peut être " le carré de
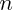
est supérieur ou égal à n ".
Si on arrive à démontrer que la validité de
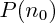
(avec
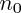
: un certain entier) entraîne la validité de
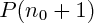
, alors il suffit de montrer que, pour un certain entier
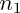
n
1, la propriété est valide, pour qu'elle soit valide à tous les rangs supérieurs à
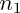
.
Ainsi, sans préjuger de la validité de
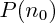
, on regarde ce que ça impliquerait au rang
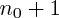
; il est tout à fait possible que la validité de
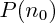
implique la validité de
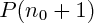
, sans que la propriété P ne soit valide pour quelqu'entier que ce soit : on reste alors dans la virtualité ; si en revanche, on montre qu'à un certain rang n, elle est vraie (en faisant le calcul, tout simplement), alors on ancre cette ribambelle de validités de propriétés dans la réalité ...
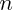 . La propriété sera notée
. La propriété sera notée 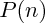 .
.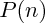 peut être " le carré de
peut être " le carré de 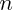 est supérieur ou égal à n ".
est supérieur ou égal à n ".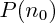 (avec
(avec 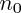 : un certain entier) entraîne la validité de
: un certain entier) entraîne la validité de 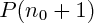 , alors il suffit de montrer que, pour un certain entier
, alors il suffit de montrer que, pour un certain entier 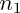 n1, la propriété est valide, pour qu'elle soit valide à tous les rangs supérieurs à
n1, la propriété est valide, pour qu'elle soit valide à tous les rangs supérieurs à 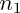 .
.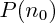 , on regarde ce que ça impliquerait au rang
, on regarde ce que ça impliquerait au rang 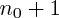 ; il est tout à fait possible que la validité de
; il est tout à fait possible que la validité de 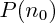 implique la validité de
implique la validité de 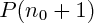 , sans que la propriété P ne soit valide pour quelqu'entier que ce soit : on reste alors dans la virtualité ; si en revanche, on montre qu'à un certain rang n, elle est vraie (en faisant le calcul, tout simplement), alors on ancre cette ribambelle de validités de propriétés dans la réalité ...
, sans que la propriété P ne soit valide pour quelqu'entier que ce soit : on reste alors dans la virtualité ; si en revanche, on montre qu'à un certain rang n, elle est vraie (en faisant le calcul, tout simplement), alors on ancre cette ribambelle de validités de propriétés dans la réalité ...