DÉFINITION
Un intervalle de R (ensemble des réels) est un ensemble de réels
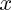
compris entre deux bornes ; ainsi, l'ensemble des réels supérieurs à 2, mais inférieurs à 3, est un intervalle.
Un intervalle peut être ouvert ou fermé à ses bornes : lorsque la borne est incluse dans l'intervalle, on dit que l'intervalle est " fermé " à cette borne ; lorsqu'elle est exclue de l'intervalle, il est dit " ouvert ".
NOTATION
L'ensemble des réels supérieurs ou égaux à 2 (l'intervalle est donc fermé en 2) mais strictement inférieurs à 3 (l'intervalle est donc ouvert en 3) est noté :
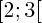
.
Propriétés
L'intersection de deux intervalles est un intervalle ; ainsi, l'intersection de
![$ [2;6] \text{~et~} [4;10] $ $ [2;6] \text{~et~} [4;10] $](/latexrender/pictures/86583fb34c423f94753444880063d710.png)
(c'est l'ensemble des réels qui appartiennent à la fois à [2 ; 6] et à [4 ; 10]) est l'intervalle
![$ [4;6] $ $ [4;6] $](/latexrender/pictures/e7c3a9af94787420fe2255067beab614.png)
Union de deux intervalles : c'est l'ensemble des réels appartenant soit à l'un, soit à l'autre, des deux intervalles ; ces deux intervalles peuvent être disjoints : ainsi, l'union de
![$ [2;3] $ $ [2;3] $](/latexrender/pictures/f611b49927efada39cd112b57aabbf92.png)
et
![$ [5;7] $ $ [5;7] $](/latexrender/pictures/6afea784fbdf7cf5f5dc64970eaa0dde.png)
est composée de l'ensemble des réels compris entre 2 et 3, et des réels compris entre 5 et 7.
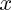 compris entre deux bornes ; ainsi, l'ensemble des réels supérieurs à 2, mais inférieurs à 3, est un intervalle.
compris entre deux bornes ; ainsi, l'ensemble des réels supérieurs à 2, mais inférieurs à 3, est un intervalle.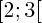 .
.![$ [2;6] \text{~et~} [4;10] $ $ [2;6] \text{~et~} [4;10] $](/latexrender/pictures/86583fb34c423f94753444880063d710.png) (c'est l'ensemble des réels qui appartiennent à la fois à [2 ; 6] et à [4 ; 10]) est l'intervalle
(c'est l'ensemble des réels qui appartiennent à la fois à [2 ; 6] et à [4 ; 10]) est l'intervalle ![$ [4;6] $ $ [4;6] $](/latexrender/pictures/e7c3a9af94787420fe2255067beab614.png)
![$ [2;3] $ $ [2;3] $](/latexrender/pictures/f611b49927efada39cd112b57aabbf92.png) et
et ![$ [5;7] $ $ [5;7] $](/latexrender/pictures/6afea784fbdf7cf5f5dc64970eaa0dde.png) est composée de l'ensemble des réels compris entre 2 et 3, et des réels compris entre 5 et 7.
est composée de l'ensemble des réels compris entre 2 et 3, et des réels compris entre 5 et 7.