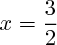DÉFINITION
Une équation est une relation d'égalité entre deux termes. Ces deux termes peuvent être des
nombres 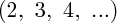
ou bien des
expressions qui dépendent de valeurs inconnues (représentées par des lettres :
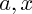
, ...).
Exemple
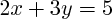
est une équation ; elle a deux inconnues :
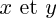
.
Une équation à une seule inconnue est dite "
du premier degré " lorsque
cette inconnue est à la puissance 1 ; par exemple :
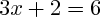
est une équation du premier degré (l'équation
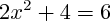
n'en est pas une).
OPÉRATIONS SUR LES ÉQUATIONS
Connaissant une équation du premier degré à une inconnue, on peut calculer cette inconnue, par des opérations sur les deux termes de l'équation.
Exemple :
soit l'équation
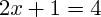
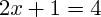
donc :
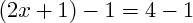
(on retranche 1 à chacun des deux termes)
donc :
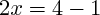
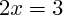
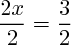
(on divise les deux termes par 2)
On a donc :
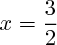
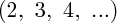 ou bien des expressions qui dépendent de valeurs inconnues (représentées par des lettres :
ou bien des expressions qui dépendent de valeurs inconnues (représentées par des lettres : 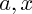 , ...).
, ...). 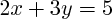 est une équation ; elle a deux inconnues :
est une équation ; elle a deux inconnues : 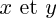 .
.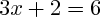 est une équation du premier degré (l'équation
est une équation du premier degré (l'équation 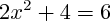 n'en est pas une).
n'en est pas une).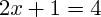
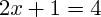
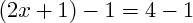 (on retranche 1 à chacun des deux termes)
(on retranche 1 à chacun des deux termes)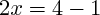
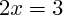
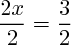 (on divise les deux termes par 2)
(on divise les deux termes par 2)