DÉFINITIONS
Soit une droite
(D) ; la
réflexion d'axe (D)(encore appelée :
symétrie d'axe (D) ) est une transformation qui associe à tout point A un point A' tel que : (AA') perpendiculaire à
(D), et (si on note I l'intersection de (AA') avec
(D)) :
AI = A'I si A appartient à
(D),
l'image de A est A lui-même.
Soit un point O ;
la symétrie de centre O est une transformation qui associe à tout point A le point A' tel que :
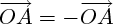
Soit un vecteur
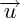
; la
translation de vecteur 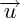
est une transformation qui associe à tout point
A le point
A' tel que :
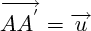
Soient un point O et un réel
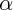 la rotation de centre O
la rotation de centre O et d'angle
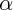
est une transformation qui associe à tout point
A un point
A' tel que :
OA =
OA' et l'angle
AOA' vaut
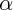
.
PROPRIÉTÉS
Toutes ces transformations conservent l'alignement, les distances, les angles, les surfaces, les milieux, le parallélisme et la perpendicularité. Ainsi, si A, B et C sont alignés, leurs images (A', B' et C') par une de ces transformations seront alignées aussi ; la distance entre A' et B' sera égale à la distance entre A et B ; si deux droites sont parallèles, leurs images seront parallèles également ;etc.
L'image d'une droite par une symétrie centrale est une droite parallèle à la première ; l'image (par n'importe laquelle des tranformations ci-dessus) du cercle de centre O et de rayon r, est le cercle de centre O' (image de O) et de rayon r.
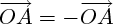
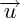 ; la translation de vecteur
; la translation de vecteur 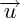 est une transformation qui associe à tout point A le point A' tel que :
est une transformation qui associe à tout point A le point A' tel que : 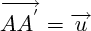
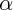 la rotation de centre O et d'angle
la rotation de centre O et d'angle 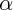 est une transformation qui associe à tout point A un point A' tel que : OA = OA' et l'angle AOA' vaut
est une transformation qui associe à tout point A un point A' tel que : OA = OA' et l'angle AOA' vaut 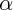 .
.