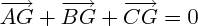SOMME DE DEUX VECTEURS
la somme de deux vecteurs est un vecteur, qui peut se construire géométriquement, en reportant l'origine d'un des deux vecteurs à la suite de l'autre.
Pour construire géométriquement la différence de deux vecteurs, par exemple :
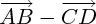
, on commence par tracer l'opposé du deuxième vecteur (c'est à dire
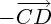
, donc :
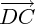
), et on le reporte à la suite du premier. On réalise donc la somme :
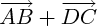
La relation de Chasles
Pour tous points A, B et C du plan, on a :
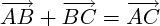
MULTIPLICATION D'UN VECTEUR PAR UN RÉEL
Soit un vecteur
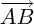
, et soit un réel

.
Le résultat de la multiplication
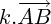
est le vecteur colinéaire à
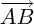
, de norme
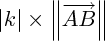
, et de sens : le même que
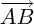
si

est positif, le sens opposé si

est négatif.
Lorsque
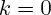
, le résultat de la multiplication de n'importe quel vecteur par

, donne le vecteur nul.
PROPRIÉTÉS GÉOMÉTRIQUES

Si I est le
milieu du segment
![$[AB]$ $[AB]$](/latexrender/pictures/c2822caf3ae4213e5c86f81ee2ed6eaa.png)
:
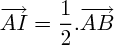
 Centre de gravité d'un triangle :
Centre de gravité d'un triangle :
soit G le centre de gravité du triangle ABC ; on a :
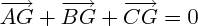
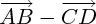 , on commence par tracer l'opposé du deuxième vecteur (c'est à dire
, on commence par tracer l'opposé du deuxième vecteur (c'est à dire 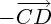 , donc :
, donc : 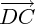 ), et on le reporte à la suite du premier. On réalise donc la somme :
), et on le reporte à la suite du premier. On réalise donc la somme : 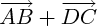
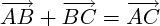
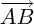 , et soit un réel
, et soit un réel  .
.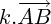 est le vecteur colinéaire à
est le vecteur colinéaire à 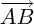 , de norme
, de norme 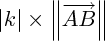 , et de sens : le même que
, et de sens : le même que 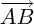 si
si  est positif, le sens opposé si
est positif, le sens opposé si  est négatif.
est négatif.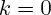 , le résultat de la multiplication de n'importe quel vecteur par
, le résultat de la multiplication de n'importe quel vecteur par  , donne le vecteur nul.
, donne le vecteur nul. Si I est le milieu du segment
Si I est le milieu du segment ![$[AB]$ $[AB]$](/latexrender/pictures/c2822caf3ae4213e5c86f81ee2ed6eaa.png) :
: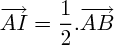
 Centre de gravité d'un triangle :
Centre de gravité d'un triangle :