DÉFINITIONS
Soient un ensemble de points
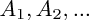
auxquels sont associés des coefficients réels
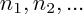
On appelle " barycentre de
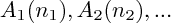
" le point G tel que :
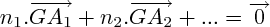
Condition à l'unicité de G
: il faut que la somme des coefficients
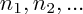
soit différente de 0 ; si elle est égale à 0, tout point M du plan vérifie la relation.
Remarque : le centre de gravité d'un triangle est le barycentre des trois sommets, associés au même coefficient non nul (c'est l' "
isobarycentre " des trois sommets).
ASSOCIATION DE BARYCENTRES
Si
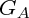
est le barycentre de
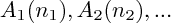
et
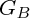
, le barycentre de
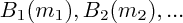
, alors le barycentre de
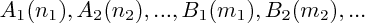
est le barycentre de
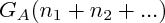
et
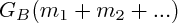
.
On peut donc " regrouper " les points, et réduire ainsi leur nombre dans les calculs.
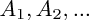 auxquels sont associés des coefficients réels
auxquels sont associés des coefficients réels 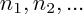
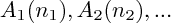 " le point G tel que :
" le point G tel que :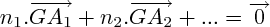
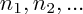 soit différente de 0 ; si elle est égale à 0, tout point M du plan vérifie la relation.
soit différente de 0 ; si elle est égale à 0, tout point M du plan vérifie la relation.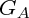 est le barycentre de
est le barycentre de 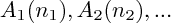 et
et 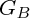 , le barycentre de
, le barycentre de 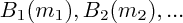 , alors le barycentre de
, alors le barycentre de 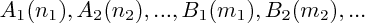 est le barycentre de
est le barycentre de 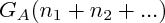 et
et 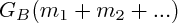 .
.