DÉFINITION
Il ne faut pas se bourrer le crâne des formules des derivées sans garder en tête la définition de la dérivation : la dérivation n'est pas seulement une baguette magique qui transforme
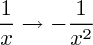
,
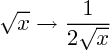
, ... , c'est avant tout la fonction qui, en tout point
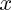
où elle est definie, prend la valeur :
![$ \lim_{h \to 0} \left( \frac{[f(x+h) - f(x)]}{h} \right) $ $ \lim_{h \to 0} \left( \frac{[f(x+h) - f(x)]}{h} \right) $](/latexrender/pictures/ededf6276a635c5bb4350ae6db6fb16c.png)
Alors bien sûr, cette formule est très peu pratique pour le calcul (et rassurez-vous, elle ne sert jamais dans les exercices : on utilise les formules des dérivées de fonctions connues, dont on parlait plus haut), mais c'est grâce a elle que vous aurez l'intuition des applications de la derivation : l'étude des variations de fonctions (puisque la derivée est, en tout point où elle est définie, la limite du taux d'accroissement de la fonction).
Il est important de garder cette vision intuitive de la dérivation, car :
- il n'y a guere qu'au début, qu'on vous demandera simplement "Calculez la derivée de cette fonction", sans aller plus loin ...
- une compréhension approfondie de la dérivation vous sera d'un grand secours en terminale, quand on vous parlera de l'intégration (le processus inverse de la dérivation, qui transforme f' en f)...
DÉRIVÉES DES FONCTIONS USUELLES
Cela dit, en faisant l'effort de garder en tête la signification de la dérivation, il vous faudra apprendre les dérivées des fonctions usuelles : dérivées des fonctions polynomiales, des fonctions qui, à
x, associent 1/
x, racine de
x,
cosinus x, sinus x.
PROPRIÉTÉS DE LA DÉRIVATION
Connaissez également les propriétes de la derivation :
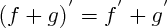
[Formule incorrecte ou erreur de parsing. Erreur 6 ]
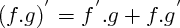
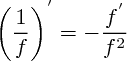
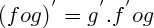
Ces formules vous permettront de retrouver les dérivées de fonctions inconnues, mais qui sont des produits, des quotients, des composées de fonctions connues. Par éfinition, f' donne les variations de f :
sur les intervalles ou f' > 0, f est strictement croissante, sur les intervalles où f' < 0, f est strictement décroissante, et sur les intervalles ou f'=0, f est constante.
APPLICATIONS
-
calculs d'optimums : en effet, pour une fonction dérivable sur un intervalle, tout optimum (maximum ou minimum) de f est un point ou s'annule f' en changeant de signe ; il suffit donc de résoudre l'équation
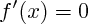
, et de vérifier le signe de f' pour x supérieur, et inférieur, à cette valeur qui annule f'
-
tableaux de variations : le signe de f' donne le sens de variations de la fonction f : il devient donc possible de déterminer les sens de variations de f, sur tous les intervalles ou elle est derivable
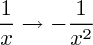 ,
, 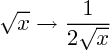 , ... , c'est avant tout la fonction qui, en tout point
, ... , c'est avant tout la fonction qui, en tout point 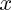 où elle est definie, prend la valeur :
où elle est definie, prend la valeur : ![$ \lim_{h \to 0} \left( \frac{[f(x+h) - f(x)]}{h} \right) $ $ \lim_{h \to 0} \left( \frac{[f(x+h) - f(x)]}{h} \right) $](/latexrender/pictures/ededf6276a635c5bb4350ae6db6fb16c.png)
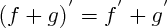
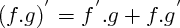
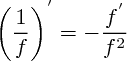
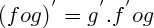
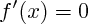 , et de vérifier le signe de f' pour x supérieur, et inférieur, à cette valeur qui annule f'
, et de vérifier le signe de f' pour x supérieur, et inférieur, à cette valeur qui annule f'