DÉFINITION
Les fonctions polynômiales sont des fonctions qui, à un réel x, associent
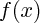
de la forme :
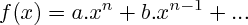
f(
x) =
axn +
bxn-1 +...
(elles ne font intervenir que des puissances entières de
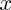
).
La puissance maximale de
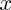
dans cette expression (l'entier
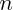
, dans l'exemple ci-dessus, avec
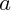
non nul) est appelée "
degré du polynôme".
Les fonctions rationnelles sont des fonctions de la forme :

où
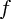
et
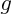
sont deux fonctions polynômiales.
Remarque
une fonction
affine est une fonction polynômiale du premier degré (de degré 1).
OPÉRATIONS SUR LES FONCTIONS
Soient
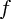
et
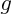
deux fonctions ;
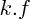
(avec

: réel) est une fonction, définie en tout point où
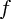
est définie ;
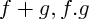
sont des fonctions, définies en tout point où
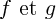
sont définies.
Si
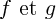
sont des fonctions polynômiales,
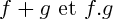
en sont aussi ; si
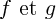
sont des fonctions rationnelles,
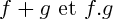
en sont aussi.
L'égalité "
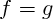
" signifie que :
1.
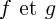
ont le même ensemble de définition ;
2. en tout point
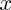
de cet ensemble :
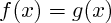
.
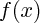 de la forme :
de la forme : 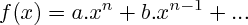
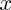 ).
).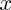 dans cette expression (l'entier
dans cette expression (l'entier 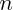 , dans l'exemple ci-dessus, avec
, dans l'exemple ci-dessus, avec 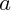 non nul) est appelée " degré du polynôme".
non nul) est appelée " degré du polynôme". où
où 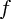 et
et 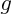 sont deux fonctions polynômiales.
sont deux fonctions polynômiales.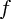 et
et 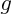 deux fonctions ;
deux fonctions ;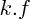 (avec
(avec  : réel) est une fonction, définie en tout point où
: réel) est une fonction, définie en tout point où 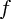 est définie ;
est définie ; 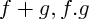 sont des fonctions, définies en tout point où
sont des fonctions, définies en tout point où 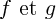 sont définies.
sont définies.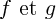 sont des fonctions polynômiales,
sont des fonctions polynômiales, 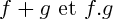 en sont aussi ; si
en sont aussi ; si 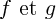 sont des fonctions rationnelles,
sont des fonctions rationnelles, 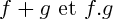 en sont aussi.
en sont aussi.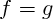 " signifie que :
" signifie que :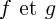 ont le même ensemble de définition ;
ont le même ensemble de définition ;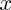 de cet ensemble :
de cet ensemble : 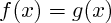 .
.