DÉFINITION
Le produit scalaire des vecteurs
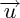
et
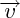
est un
réel ; il est noté :
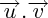
Il est égal au
produit des normes des deux vecteurs, multiplié par le cosinus de l'angle qu'ils font l'un par rapport à l'autre.
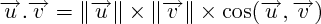
Expression analytique
Si le vecteur
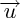
a pour coordonnées
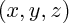
(ou, si on travaille dans le plan :
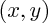
) et si le vecteur
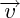
a pour coordonnées
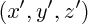
(dans le plan :
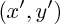
), alors leur produit scalaire vaut :
xx'+
yy'+
zz' (dans le plan : xx'+yy').
PROPRIÉTÉS

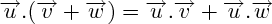
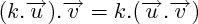
où
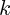
est un réel
APPLICATIONS
Calcul de distances, de surfaces, de volumes.
Exemple : calcul de la distance du point A à la droite (D), de vecteur directeur 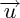 :
:
Cette distance est la distance entre A et le projeté orthogonal de A sur
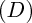
(on va le noter : H). On a donc
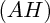
perpendiculaire à
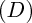
; en terme de vecteurs :
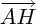
orthogonal à
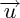
ce qui veut dire
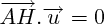
On connaît les coordonnées de
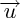
, donc, connaissant le produit scalaire, on en déduit une relation entre l'abscisse et l'ordonnée de
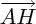
, donc, entre l'abscisse et l'ordonnée de
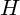
; comme de plus
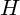
appartient à
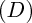
, on dispose d'une relation supplémentaire entre son abscisse et son ordonnée : il ne reste qu'à résoudre un système de deux équations à deux inconnues pour trouver les coordonnées de
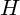
, et donc, calculer la distance
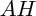
.
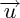 et
et 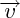 est un réel ; il est noté :
est un réel ; il est noté :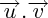
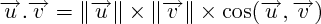
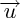 a pour coordonnées
a pour coordonnées 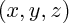 (ou, si on travaille dans le plan :
(ou, si on travaille dans le plan : 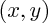 ) et si le vecteur
) et si le vecteur 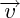 a pour coordonnées
a pour coordonnées 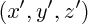 (dans le plan :
(dans le plan : 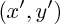 ), alors leur produit scalaire vaut : xx'+yy'+zz' (dans le plan : xx'+yy').
), alors leur produit scalaire vaut : xx'+yy'+zz' (dans le plan : xx'+yy').
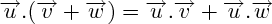
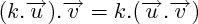 où
où 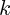 est un réel
est un réel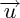 :
: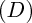 (on va le noter : H). On a donc
(on va le noter : H). On a donc 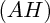 perpendiculaire à
perpendiculaire à 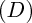 ; en terme de vecteurs :
; en terme de vecteurs :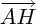 orthogonal à
orthogonal à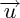 ce qui veut dire
ce qui veut dire 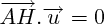
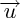 , donc, connaissant le produit scalaire, on en déduit une relation entre l'abscisse et l'ordonnée de
, donc, connaissant le produit scalaire, on en déduit une relation entre l'abscisse et l'ordonnée de 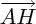 , donc, entre l'abscisse et l'ordonnée de
, donc, entre l'abscisse et l'ordonnée de 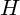 ; comme de plus
; comme de plus 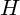 appartient à
appartient à 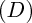 , on dispose d'une relation supplémentaire entre son abscisse et son ordonnée : il ne reste qu'à résoudre un système de deux équations à deux inconnues pour trouver les coordonnées de
, on dispose d'une relation supplémentaire entre son abscisse et son ordonnée : il ne reste qu'à résoudre un système de deux équations à deux inconnues pour trouver les coordonnées de 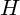 , et donc, calculer la distance
, et donc, calculer la distance 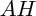 .
.