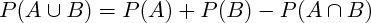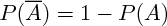VOCABULAIRE
Éventualité
On appelle "éventualité" le résultat d'une mesure (exemple : on lance un dé, et on regarde le résultat ; " le résultat est 5 " est une éventualité). On appelle " événement " un ensemble d'éventualités (exemple, dans le cas du dé : " le résultat est un nombre impair " est un événement ; cet événement est l'ensemble des éventualités " le résultat est 1 ", " le résultat est 3 " et " le résultat est 5 ").
Univers des possibles
On appelle "univers des possibles" (ou, plus modestement, " univers ") l'ensemble des éventualités réalisables (dans le cas du dé, il y a six éventualitésréalisables).
Equiprobabilité
on dit qu'il y a équiprobabilité lorsque toutes les éventualités ont la même probabilité d'arriver (dans l'exemple du dé : il y a équiprobabilité si le dé est correctement équilibré). Dans ce cas, la probabilité de chaque éventualité vaut : 1/card(univers). Dans les cas où il n'y a pas équiprobabilité, il faut faire des mesures statistiques pour avoir une idée des probabilités de chaque éventualité.
NOTATIONS
L'intersection de deux événements A et B est appelée "A inter B", et est notée :
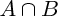
La réunion de deux événements A et B (c'est l'événement "soit A est réalisé, soit B est réalisé") est appelée "A union B", et est notée :
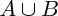
.
L'événement contraire de l'événement A est noté :
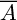
.
PROBABILITÉ D'UN ÉVÉNEMENT
La probabilité de l'événement A est égale à la somme des probabilités de chacune des éventualités qui réalisent A (remarque : on a donc, dans le cas de l'équiprobabilité :
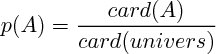
, puisqu'il y a card(A) éventualités qui réalisent A).
La probabilité d'une union d'événements vaut :
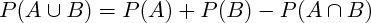
La probabilité de l'événement contraire de A vaut :
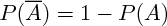
.
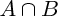
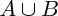 .
.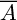 .
.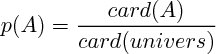 , puisqu'il y a card(A) éventualités qui réalisent A).
, puisqu'il y a card(A) éventualités qui réalisent A).