ANGLES ORIENTÉS
Lorsque le plan est orienté, il est possible de définir un sens pour les angles (on oriente le plan en indiquant, sur le schéma, le sens dans lequel tournent les angles positifs).
LE CERCLE TRIGONOMÉTRIQUE
C'est la représentation graphique du sinus et du cosinus des angles ; moyennant un petit ajout, on peut même y faire apparaître la tangente ... Il est utile de le connaître par coeur, ça aide à retrouver rapidement la valeur (ou bien, l'ordre de grandeur) du sinus ou du cosinus d'un angle donné.
COSINUS ET SINUS DE SOMMES ET DE DIFFÉRENCES
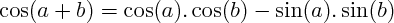
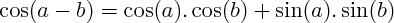
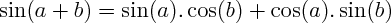
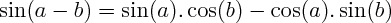
On utilise les formules de
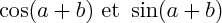
pour calculer
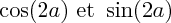
cos(2
a) et sin(2
a), en posant

:
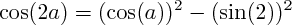
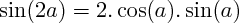
Dans un plan orienté, les
rotations (définies par un
centre, et un
angle, qui peut donc être positif ou négatif) transforment chaque point M en un point M' unique, tel que (si on note O le centre de la rotation et
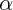
son angle) :
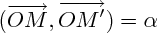
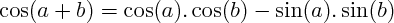
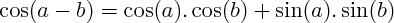
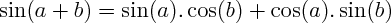
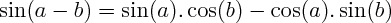
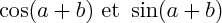 pour calculer
pour calculer 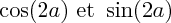 cos(2a) et sin(2a), en posant
cos(2a) et sin(2a), en posant  :
: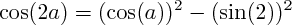
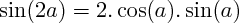
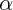 son angle) :
son angle) :