LES ÉQUATIONS DU SECOND DEGRÉ
Ce sont des équations dans laquelle l'inconnue est à la puissance 2, et éventuellement à des puissances inférieures. Exemple :
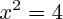
est une équation du second degré, mais aussi
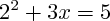
(qui fait intervenir
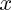
).
MÉTHODES DE RÉSOLUTION D'UNE ÉQUATION DU SECOND DEGRÉ
1. En utilisant les formes canoniques
On ramène l'équation à une forme

, ou bien :
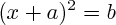
; ces équations sont ensuite simples à résoudre.
Si
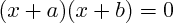
par exemple, les solutions sont de façon évidente
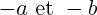
.
Si
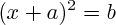
, il n'y a pas de solution si

, une solution si

(c'est -a), deux solutions si

: il suffit de passer b dans l'autre membre de l'équation et de reconnaître une identité remarquable de la forme
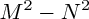
2. Lorsqu'il est impossible de se ramener à une forme canonique
, ou qu'il n'est pas évident de trouver a et b tels que :
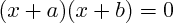
: on calcule le
discriminant de l'équation ; son signe nous renseigne sur le nombre de solutions (aussi appelées :
racines), et sa valeur nous donne les solutions éventuelles.
LE DISCRIMINANT
Soit l'équation :
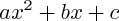
(avec
a non nul). Le discriminant

vaut :
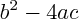
.
Si

: l'équation n'admet aucune racine réelle.
Si
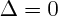
: elle admet une unique racine, la " racine double ", qui vaut :
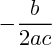
Si

: elle admet deux racines réelles, qui valent :
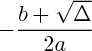
et
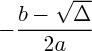
- Lorsque l'équation n'admet pas de racine réelle (cas "
 "), l'expression
"), l'expression 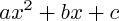 est du signe de
est du signe de 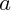 sur l'ensemble des réels.
sur l'ensemble des réels.
- Lorsque l'équation admet une racine double (cas "
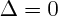 "), l'expression
"), l'expression 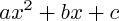 est du signe de
est du signe de 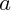 sur l'ensemble des réels sauf à la racine, où elle est évidemment nulle (par définition de la racine).
sur l'ensemble des réels sauf à la racine, où elle est évidemment nulle (par définition de la racine).
- Lorsque l'équation admet deux racines réelles (cas "
 "), l'expression
"), l'expression 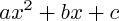 est du signe de
est du signe de 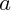 en-dehors de l'intervalle des racines, elle est de signe opposée entre les racines, et naturellement (par définition des racines), elle s'annule à chacune des deux racines.
en-dehors de l'intervalle des racines, elle est de signe opposée entre les racines, et naturellement (par définition des racines), elle s'annule à chacune des deux racines.
Ces propriétés permettent de résoudre les inéquations du second degré. Par exemple, pour résoudre "
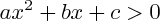
", on étudie l'existence et le nombre des racines de l'équation
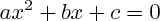
; les propriétés ci-dessus permettent de déterminer sur quels ensembles l'expression
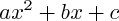
est strictement positive.
FONCTIONS POLYNÔMIALES DU SECOND DEGRÉ
Ce sont des fonctions de la forme :
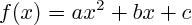
; l'étude du signe de ces fonctions se ramène donc à des résolutions d'équations du second degré.
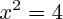 est une équation du second degré, mais aussi
est une équation du second degré, mais aussi 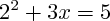 (qui fait intervenir
(qui fait intervenir 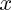 ).
). , ou bien :
, ou bien : 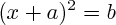 ; ces équations sont ensuite simples à résoudre.
; ces équations sont ensuite simples à résoudre.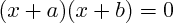 par exemple, les solutions sont de façon évidente
par exemple, les solutions sont de façon évidente 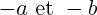 .
.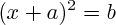 , il n'y a pas de solution si
, il n'y a pas de solution si  , une solution si
, une solution si  (c'est -a), deux solutions si
(c'est -a), deux solutions si  : il suffit de passer b dans l'autre membre de l'équation et de reconnaître une identité remarquable de la forme
: il suffit de passer b dans l'autre membre de l'équation et de reconnaître une identité remarquable de la forme 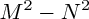
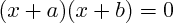 : on calcule le discriminant de l'équation ; son signe nous renseigne sur le nombre de solutions (aussi appelées : racines), et sa valeur nous donne les solutions éventuelles.
: on calcule le discriminant de l'équation ; son signe nous renseigne sur le nombre de solutions (aussi appelées : racines), et sa valeur nous donne les solutions éventuelles.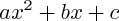
 vaut :
vaut : 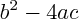 .
. : l'équation n'admet aucune racine réelle.
: l'équation n'admet aucune racine réelle.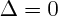 : elle admet une unique racine, la " racine double ", qui vaut :
: elle admet une unique racine, la " racine double ", qui vaut : 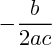
 : elle admet deux racines réelles, qui valent :
: elle admet deux racines réelles, qui valent : 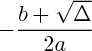 et
et 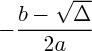
 "), l'expression
"), l'expression 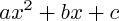 est du signe de
est du signe de 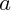 sur l'ensemble des réels.
sur l'ensemble des réels.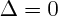 "), l'expression
"), l'expression 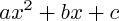 est du signe de
est du signe de 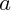 sur l'ensemble des réels sauf à la racine, où elle est évidemment nulle (par définition de la racine).
sur l'ensemble des réels sauf à la racine, où elle est évidemment nulle (par définition de la racine). "), l'expression
"), l'expression 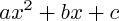 est du signe de
est du signe de 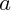 en-dehors de l'intervalle des racines, elle est de signe opposée entre les racines, et naturellement (par définition des racines), elle s'annule à chacune des deux racines.
en-dehors de l'intervalle des racines, elle est de signe opposée entre les racines, et naturellement (par définition des racines), elle s'annule à chacune des deux racines.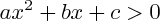 ", on étudie l'existence et le nombre des racines de l'équation
", on étudie l'existence et le nombre des racines de l'équation 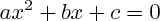 ; les propriétés ci-dessus permettent de déterminer sur quels ensembles l'expression
; les propriétés ci-dessus permettent de déterminer sur quels ensembles l'expression 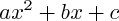 est strictement positive.
est strictement positive.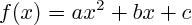 ; l'étude du signe de ces fonctions se ramène donc à des résolutions d'équations du second degré.
; l'étude du signe de ces fonctions se ramène donc à des résolutions d'équations du second degré.