
Dm de mathématique
Mathematiques > sujets expliqués - 02/11/2013 - correction
    
|
Bonjour,
EXERCICE 2 :
Pour la correction de cet exercice je te donne donc les réponses sans explication pour que tu vérifies avec ce que tu as fait, et si t'as des questions demandes moi.
a. Pour x=0 et x=3. Points d'intersection : (0;3) et (3;0)
b. x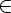
![$\left]0;3\right[$ $\left]0;3\right[$](/latexrender/pictures/89bcb28f639c8bd900e019c6c2b826ce.png)
c. x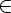
![$\left]-\infty ;0\right]\cup \left[3;+\infty \right[$ $\left]-\infty ;0\right]\cup \left[3;+\infty \right[$](/latexrender/pictures/9998f645e2e2b81ee3cb12356f290cde.png)
EXERCICE 3 :
1) Je te le fais pour le point A pour te montrer comment faire et je te laisse faire pour les points B et C.
On a f(x) =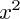 - 5x + 6
- 5x + 6
On veut montrer que A (1;2) appartient à Cf.
Il suffit de montrer que l'image de 1 par f donne bien 2, donc que f(1)=2.
Calculons : f(1) =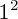 - 5.1 + 6 = 1 - 5 + 6 = 7 - 5 = 2
- 5.1 + 6 = 1 - 5 + 6 = 7 - 5 = 2
Ok, on a bien démontré ce que l'on voulait, donc A appartient à Cf.
De même pour B il faut que tu montres que f(-3)=31 et pour C que f(4/3)=10/9
2) On cherche le point d'intersection entre la courbe de f et l'axe des ordonnées.
L'axe des ordonnées étant l'axe vertical central, il se caractérise par x = 0. Donc pour tout point de l'axe x=0. Or si l'on veut que ce point appartienne aussi à Cf, il faut qu'il ait pour coordonnées (x;f(x)).
On vient de dire que x=0, donc calculons f(0) pour avoir l'ordonnée de ce point :
f(0)=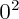 - 5.0 + 6 = 6
- 5.0 + 6 = 6
Le point d'intersection a donc pour coordonnées (0;6).
3) a. Pour démontrer la relation, on va développer (x-2)(x-3) et montrer que ça vaut bien f(x).
(x-2)(x-3) = x.x - 3x - 2x - 2.3 =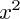 - 5x + 6 ce qui vaut bien f(x) !
- 5x + 6 ce qui vaut bien f(x) !
b.On cherche maintenant les points d'intersection entre la courbe de f et l'axe des abscisses.
L'axe des abscisses étant l'axe horizontal centré, il se caractérise par y=0 en tout point de l'axe.
Donc tout point de l'axe a pour coordonnées (x;0). Or si l'on veut que ce point appartienne aussi à Cf, il faut qu'il ait pour coordonnées (x;f(x)).
Un point n'ayant qu'une seule image possible, il nous faut f(x)=0. Cherchons x qui réponde à cette équation.
On utilise la forme trouvée précédemment pour f, soit :
(x-2)(x-3) = 0.
Alors on sait (dans ton cours normalement) que cela revient à dire : (x-2) = 0 ou (x-3) = 0
Donc x=2 ou x=3.
La courbe de f a donc deux points d'intersection avec l'axe des abscisses, ayant pour coordonnées (2;0) et (3;0).
EXERCICE 4 :
a. Les variables sont les valeurs que l'on peut choisir de faire varier, que l'on peut modifier nous même. Ce sont donc les valeurs d'entrée de l'algorithme : a et b.
b. Pour a=2 et b=1.
Première question : a-t-on a>b ? Oui.
Alors m prend la valeur de a, donc m=2.
L'algorithme nous sort la valeur 2.
c. Pour a=2 et b=8.
A-t-on a>b ? Non.
Alors c'est l'option "sinon" de l'algorithme, et donc m vaut b. Donc la valeur en sortie est 8.
d. Pour a = 10 et b = 10.
A-t-on a>b ? Non. Attention, l'inégalité ici est stricte ! Comme les valeurs sont égales, on n'a pas a>b. Donc c'est l'option "sinon", et m prend la valeur de b. Ici cela revient au même puisque a=b, donc on aurait la même valeur en sortie de l'algorithme mais il faut toujours penser à faire bien attention aux sens des inégalités !
Et donc en valeur de sortie on obtient 10.
e. Avec les trois exemples on voit que la valeur qui ressort est toujours la valeur maximum parmi les deux valeurs d'entrée.
De façon générale, si a>b, l'algorithme nous donne a, qui est bien le maximum entre a et b.
Et si a n'est pas > b alors ça veut dire soit que a=b (auquel cas la valeur de sortie est la même), soit que b > a. Et la valeur qui sort est b, qui est donc bien la valeur maximum entre a et b.
Cet algorithme sert donc à déterminer le maximum de deux nombres.
Cordialement,
EXERCICE 2 :
Pour la correction de cet exercice je te donne donc les réponses sans explication pour que tu vérifies avec ce que tu as fait, et si t'as des questions demandes moi.
a. Pour x=0 et x=3. Points d'intersection : (0;3) et (3;0)
b. x
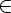
![$\left]0;3\right[$ $\left]0;3\right[$](/latexrender/pictures/89bcb28f639c8bd900e019c6c2b826ce.png)
c. x
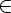
![$\left]-\infty ;0\right]\cup \left[3;+\infty \right[$ $\left]-\infty ;0\right]\cup \left[3;+\infty \right[$](/latexrender/pictures/9998f645e2e2b81ee3cb12356f290cde.png)
EXERCICE 3 :
1) Je te le fais pour le point A pour te montrer comment faire et je te laisse faire pour les points B et C.
On a f(x) =
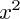 - 5x + 6
- 5x + 6On veut montrer que A (1;2) appartient à Cf.
Il suffit de montrer que l'image de 1 par f donne bien 2, donc que f(1)=2.
Calculons : f(1) =
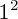 - 5.1 + 6 = 1 - 5 + 6 = 7 - 5 = 2
- 5.1 + 6 = 1 - 5 + 6 = 7 - 5 = 2Ok, on a bien démontré ce que l'on voulait, donc A appartient à Cf.
De même pour B il faut que tu montres que f(-3)=31 et pour C que f(4/3)=10/9
2) On cherche le point d'intersection entre la courbe de f et l'axe des ordonnées.
L'axe des ordonnées étant l'axe vertical central, il se caractérise par x = 0. Donc pour tout point de l'axe x=0. Or si l'on veut que ce point appartienne aussi à Cf, il faut qu'il ait pour coordonnées (x;f(x)).
On vient de dire que x=0, donc calculons f(0) pour avoir l'ordonnée de ce point :
f(0)=
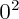 - 5.0 + 6 = 6
- 5.0 + 6 = 6Le point d'intersection a donc pour coordonnées (0;6).
3) a. Pour démontrer la relation, on va développer (x-2)(x-3) et montrer que ça vaut bien f(x).
(x-2)(x-3) = x.x - 3x - 2x - 2.3 =
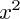 - 5x + 6 ce qui vaut bien f(x) !
- 5x + 6 ce qui vaut bien f(x) ! b.On cherche maintenant les points d'intersection entre la courbe de f et l'axe des abscisses.
L'axe des abscisses étant l'axe horizontal centré, il se caractérise par y=0 en tout point de l'axe.
Donc tout point de l'axe a pour coordonnées (x;0). Or si l'on veut que ce point appartienne aussi à Cf, il faut qu'il ait pour coordonnées (x;f(x)).
Un point n'ayant qu'une seule image possible, il nous faut f(x)=0. Cherchons x qui réponde à cette équation.
On utilise la forme trouvée précédemment pour f, soit :
(x-2)(x-3) = 0.
Alors on sait (dans ton cours normalement) que cela revient à dire : (x-2) = 0 ou (x-3) = 0
Donc x=2 ou x=3.
La courbe de f a donc deux points d'intersection avec l'axe des abscisses, ayant pour coordonnées (2;0) et (3;0).
EXERCICE 4 :
a. Les variables sont les valeurs que l'on peut choisir de faire varier, que l'on peut modifier nous même. Ce sont donc les valeurs d'entrée de l'algorithme : a et b.
b. Pour a=2 et b=1.
Première question : a-t-on a>b ? Oui.
Alors m prend la valeur de a, donc m=2.
L'algorithme nous sort la valeur 2.
c. Pour a=2 et b=8.
A-t-on a>b ? Non.
Alors c'est l'option "sinon" de l'algorithme, et donc m vaut b. Donc la valeur en sortie est 8.
d. Pour a = 10 et b = 10.
A-t-on a>b ? Non. Attention, l'inégalité ici est stricte ! Comme les valeurs sont égales, on n'a pas a>b. Donc c'est l'option "sinon", et m prend la valeur de b. Ici cela revient au même puisque a=b, donc on aurait la même valeur en sortie de l'algorithme mais il faut toujours penser à faire bien attention aux sens des inégalités !
Et donc en valeur de sortie on obtient 10.
e. Avec les trois exemples on voit que la valeur qui ressort est toujours la valeur maximum parmi les deux valeurs d'entrée.
De façon générale, si a>b, l'algorithme nous donne a, qui est bien le maximum entre a et b.
Et si a n'est pas > b alors ça veut dire soit que a=b (auquel cas la valeur de sortie est la même), soit que b > a. Et la valeur qui sort est b, qui est donc bien la valeur maximum entre a et b.
Cet algorithme sert donc à déterminer le maximum de deux nombres.
Cordialement,
| Documents attachés : | aucun document joint. |




