
Fonction
Mathematiques > sujets expliqués - 09/04/2009 - correction
    
|
 | fonction revenir au plan | docs | ||
| Bonjour, Est-ce que je pour lire |  | |||
 | Bonjour, juste pour être s lire | |||
| C'est la 2), étant f(x)= 1/(x lire | ||||
 | Bonsoir, Méthode : lire | |||
Bonsoir,
Méthode :
- Etudier les variations de la fonction (qui sont données ici) et ses symétries.
Ici on remarque que la fonction est paire (c'est à dire f(-x)=f(x)) ce qui implique que la courbe C associée est symétrique par rapport à l'axe des ordonnées.
- Etudier les limites de la fonction aux bornes de son domaine de définition.
Ici on voit que f est définie sur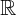 tout entier puisque
tout entier puisque 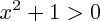 .
.
On regarde donc ses limites en + et - l'infini.
- Etudier les points particuliers (extremums de la fonction)
Ici on voit que f est maximale en 0 et prend la valeur 1 (et non pas 3 comme sur ton dessin).
On calcule aussi les valeurs de la fonction pour les points données : x = 1/4, x=1/2, x=3/4...
Une fois que tu as fait tout ça :
- Tu places les points particuliers sur le repère.
- Tu traces la courbe qui respecte les limites, les variations, les extremums et les symétries.
Si tu appliques à la lettre cette methode tu ne peux pas te tromper.
Récapitulatif conernant ton dessin :
- Tu as bien dessiné la parité de la fonction et respecté les variations.
Cependant sur ton dessin on a l'impression que les limites en + et - l'infini sont 1 ou 1/2 ce qui est faux.
De plus tu ne respectes pas les valeurs des points particuliers.
Je pense que tu as du tracer l'allure de la courbe et que tu ne comprends pas comment y rajouter les points qui ne sont pas dessus.
Commence par placer les points et trace la courbe ensuite.
(Remarque : on te fait calculer les points d'abscisse 1/4, 1/2, 3/4, 1 et 2; tu connais donc par parité les points d'abscisse -1/4, -1/2, -3/4, -1 et -2 ! Pense à les mettre ça t'aidera à tracer la courbe et se sera apprécié par le professeur.)
Bon courage !
(cf en bas pour les quelques valeurs à calculer. Ne regarde qu'après avoir fait les calculs.)
__________________________________
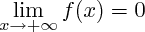
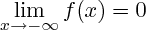
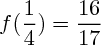
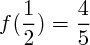
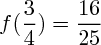
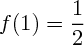
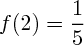
Méthode :
- Etudier les variations de la fonction (qui sont données ici) et ses symétries.
Ici on remarque que la fonction est paire (c'est à dire f(-x)=f(x)) ce qui implique que la courbe C associée est symétrique par rapport à l'axe des ordonnées.
- Etudier les limites de la fonction aux bornes de son domaine de définition.
Ici on voit que f est définie sur
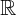 tout entier puisque
tout entier puisque 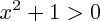 .
.On regarde donc ses limites en + et - l'infini.
- Etudier les points particuliers (extremums de la fonction)
Ici on voit que f est maximale en 0 et prend la valeur 1 (et non pas 3 comme sur ton dessin).
On calcule aussi les valeurs de la fonction pour les points données : x = 1/4, x=1/2, x=3/4...
Une fois que tu as fait tout ça :
- Tu places les points particuliers sur le repère.
- Tu traces la courbe qui respecte les limites, les variations, les extremums et les symétries.
Si tu appliques à la lettre cette methode tu ne peux pas te tromper.
Récapitulatif conernant ton dessin :
- Tu as bien dessiné la parité de la fonction et respecté les variations.
Cependant sur ton dessin on a l'impression que les limites en + et - l'infini sont 1 ou 1/2 ce qui est faux.
De plus tu ne respectes pas les valeurs des points particuliers.
Je pense que tu as du tracer l'allure de la courbe et que tu ne comprends pas comment y rajouter les points qui ne sont pas dessus.
Commence par placer les points et trace la courbe ensuite.
(Remarque : on te fait calculer les points d'abscisse 1/4, 1/2, 3/4, 1 et 2; tu connais donc par parité les points d'abscisse -1/4, -1/2, -3/4, -1 et -2 ! Pense à les mettre ça t'aidera à tracer la courbe et se sera apprécié par le professeur.)
Bon courage !
(cf en bas pour les quelques valeurs à calculer. Ne regarde qu'après avoir fait les calculs.)
__________________________________
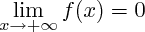
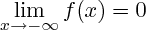
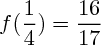
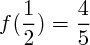
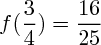
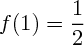
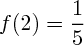
| Documents attachés : | aucun document joint. |

