
Vecteurs
Mathematiques > sujets expliqués - 27/03/2009 - correction
    
|
Bonsoir,
Malheureusement tes résultats sont erronés.
Je vais donc t'expliquer comment tout cela fonctionne afin que tu n'es plus aucun problème avec ce type d'exercice.
Lorsque l'on se place dans un repère orthonormé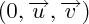 classique, et qu'on dit que le point M a pour coordonnées (3,4) cela signifie que
classique, et qu'on dit que le point M a pour coordonnées (3,4) cela signifie que 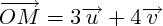
On exprime donc la position du point par rapport à une origine et en fonction de deux vecteurs de référence.
Si le repère est ici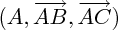 sela signifie que pour exprimer les coodonnées d'un point M il faut calculer
sela signifie que pour exprimer les coodonnées d'un point M il faut calculer 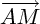 en fonction de
en fonction de 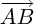 et
et 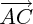
Par exemple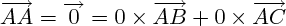 d'où le point A a bien pour coordonnées (0,0).
d'où le point A a bien pour coordonnées (0,0).
Pour le point D la démarche est similaire :
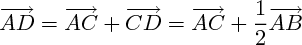
(En appliquant la relation de Chalses puis en utilisant l'égalité donnée par l'énoncé).
D'où les coordonnées (1/2,1).
Si tu as bien compris la définition de base des coordonnées d'un point dans un repère tu ne devrais plus avoir de problèmes avec ça.
Bon courage pour les autres calculs !
(Réponses tout en bas. Ne regarde que pour vérifier !)
______________________________
A(0,0)
B(1,0)
C(0,1)
D(1/2,1)
E(1,1/2)
I(1/2;1/2)
J(3/4,3/4)
Malheureusement tes résultats sont erronés.
Je vais donc t'expliquer comment tout cela fonctionne afin que tu n'es plus aucun problème avec ce type d'exercice.
Lorsque l'on se place dans un repère orthonormé
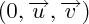 classique, et qu'on dit que le point M a pour coordonnées (3,4) cela signifie que
classique, et qu'on dit que le point M a pour coordonnées (3,4) cela signifie que 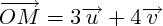
On exprime donc la position du point par rapport à une origine et en fonction de deux vecteurs de référence.
Si le repère est ici
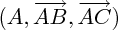 sela signifie que pour exprimer les coodonnées d'un point M il faut calculer
sela signifie que pour exprimer les coodonnées d'un point M il faut calculer 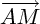 en fonction de
en fonction de 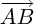 et
et 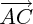
Par exemple
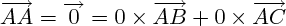 d'où le point A a bien pour coordonnées (0,0).
d'où le point A a bien pour coordonnées (0,0).Pour le point D la démarche est similaire :
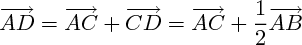
(En appliquant la relation de Chalses puis en utilisant l'égalité donnée par l'énoncé).
D'où les coordonnées (1/2,1).
Si tu as bien compris la définition de base des coordonnées d'un point dans un repère tu ne devrais plus avoir de problèmes avec ça.
Bon courage pour les autres calculs !
(Réponses tout en bas. Ne regarde que pour vérifier !)
______________________________
A(0,0)
B(1,0)
C(0,1)
D(1/2,1)
E(1,1/2)
I(1/2;1/2)
J(3/4,3/4)
| Documents attachés : | aucun document joint. |



