
Géométrie dans l'espace
Mathematiques > sujets expliqués - 28/11/2008 - Question simple
    
|
 | géométrie dans l'espace revenir au plan | docs | ||
| dans le repère usuel on se do lire | ||||
 | On cherche le(s) plan(s) (P) d lire | |||
On cherche le(s) plan(s) (P) d'équation ax+by+cz+d=0.
On cherche donc à déterminer (a,b,c,d). (a,b,c) est un vecteur normal de P.
Exploitons les hypothèses :
-> (D) appartient à (P), donc son vecteur directeur et orthogonal à (a,b,c). Le vecteur directeur de D est trouvé en mettant son équation sous forme paramétrique par exemple : (0,1,1) est un vecteur directeur de D. Il est orthogonal à (a,b,c), ce qui donne la première équation : b+c=0
->P coupe P1 et P2 suivant deux droites orthogonales. Ces droites sont d'équations :
ax+by+cz+d=0
y=5x
et
ax+by+cz+d=0
y=-5x
on trouve un de leurs vecteurs directeurs, respectivement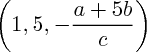 et
et 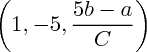 par exemple.
par exemple.
On écrit ensuite que ces vecteurs sont orthogonaux, ce qui donne la seconde équation : 25b²-a² = -24c²
-> on résout alors le système formé par ces deux équations, et on trouve : b= -c, a=7b ou a = -7b
L'équation de P est alors (7x+y-z)b +d = 0 ou (-7x +y-z)b+d=0.
Prenons le point (7/6, -8/3,0) dont on sait qu'il appartient à P (car il appartient à D) et injectons ses coordonnées dans les équations. Pour la première, cela mène à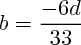 , pour la seconde à
, pour la seconde à 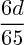 .
.
On trouve ainsi que les deux plans répondant aux hypothèses sont ceux d'équations :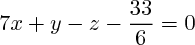 et
et 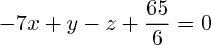
Voilà, j'espère ne pas m'être trompé dans les calculs.
On cherche donc à déterminer (a,b,c,d). (a,b,c) est un vecteur normal de P.
Exploitons les hypothèses :
-> (D) appartient à (P), donc son vecteur directeur et orthogonal à (a,b,c). Le vecteur directeur de D est trouvé en mettant son équation sous forme paramétrique par exemple : (0,1,1) est un vecteur directeur de D. Il est orthogonal à (a,b,c), ce qui donne la première équation : b+c=0
->P coupe P1 et P2 suivant deux droites orthogonales. Ces droites sont d'équations :
ax+by+cz+d=0
y=5x
et
ax+by+cz+d=0
y=-5x
on trouve un de leurs vecteurs directeurs, respectivement
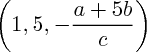 et
et 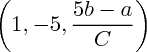 par exemple.
par exemple.On écrit ensuite que ces vecteurs sont orthogonaux, ce qui donne la seconde équation : 25b²-a² = -24c²
-> on résout alors le système formé par ces deux équations, et on trouve : b= -c, a=7b ou a = -7b
L'équation de P est alors (7x+y-z)b +d = 0 ou (-7x +y-z)b+d=0.
Prenons le point (7/6, -8/3,0) dont on sait qu'il appartient à P (car il appartient à D) et injectons ses coordonnées dans les équations. Pour la première, cela mène à
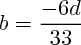 , pour la seconde à
, pour la seconde à 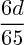 .
.On trouve ainsi que les deux plans répondant aux hypothèses sont ceux d'équations :
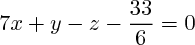 et
et 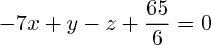
Voilà, j'espère ne pas m'être trompé dans les calculs.
| Documents attachés : | aucun document joint. |

