
Inversion plane
Mathematiques > sujets expliqués - 11/11/2008 - Question simple
    
|
 | inversion plane revenir au plan | docs | ||
| soit z = a + ib (a,b) E R² o lire | ||||
 | Il y a plusieurs façons de r� lire | |||
Il y a plusieurs façons de résoudre cette question. La première qui me vient à l'esprit est la suivante :
Remarquons que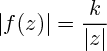
Soit M le point d'affixe z appartenant à la droite D.
Comme D ne passe pas par l'origine,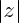 admet un minimum strictement positif lorsque M parcourt D. Par conséquent,
admet un minimum strictement positif lorsque M parcourt D. Par conséquent, 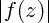 admet un maximum.
admet un maximum.
On utilise ensuite le fait que l'on connaisse le résultat à trouver, à savoir que f(D) est un cercle passant par O, pour intuiter quel sera le centre de ce cercle :
Le point réalisant le maximum du module de f(z) sera le point de f(D) le plus éloigné de O, donc le point diamétralement opposé. Pour trouver ce point, il suffit de calculer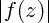 en fonction de x en écrivant z= x+iy (on a y en fonction de x grâce à l'équation de la droite).
en fonction de x en écrivant z= x+iy (on a y en fonction de x grâce à l'équation de la droite).
On trouve : [Formule incorrecte ou erreur de parsing. Erreur 6 ] (sauf erreur de ma part)
En calculant le minimum du polynôme du dénominateur, on trouve l'abscisse du point réalisant le maximum du module de f(z), l'ordonnée est trouvée en utilisant l'équation de D.
En divisant ces coordonnées par deux, on trouve donc les coordonnées du centre présumé du cercle que l'on veut trouver. Tout ceci était en fait un travail préparatoire au brouillon (l'analyse). Ensuite, la synthèse :
On calcule le module de la différence entre f(z) et l'affixe du point que l'on vient de déterminer, et on trouve normalement une constante (indépendante de x et y) ! Ce qui permet de conclure que f(D) est bien le cercle de centre le point que l'on vient de déterminer. Ce cercle est privé de O car O ne peut effectivement pas appartenir à f(D), le module de f(z) étant toujours non nul.
Voilà, cette solution est un peu calculatoire, surtout qu'on raisonne sur une droite générale d'équation ax + by + c. Je ne parviens malheureusement pas à imaginer une solution permettant de conclure plus vite.
En ce qui concerne l'image d'un cercle de centre O :
Lorsque M parcourt ce cercle, le module de z reste constant. Donc il en est de même pour le module de f(z) (qui vaut rappelons le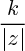 ). Donc l'image d'un cercle de centre O est un autre cercle de centre O (de rayon
). Donc l'image d'un cercle de centre O est un autre cercle de centre O (de rayon 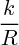 où R est le rayon du premier cercle).
où R est le rayon du premier cercle).
Remarquons que
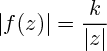
Soit M le point d'affixe z appartenant à la droite D.
Comme D ne passe pas par l'origine,
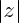 admet un minimum strictement positif lorsque M parcourt D. Par conséquent,
admet un minimum strictement positif lorsque M parcourt D. Par conséquent, 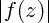 admet un maximum.
admet un maximum.On utilise ensuite le fait que l'on connaisse le résultat à trouver, à savoir que f(D) est un cercle passant par O, pour intuiter quel sera le centre de ce cercle :
Le point réalisant le maximum du module de f(z) sera le point de f(D) le plus éloigné de O, donc le point diamétralement opposé. Pour trouver ce point, il suffit de calculer
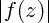 en fonction de x en écrivant z= x+iy (on a y en fonction de x grâce à l'équation de la droite).
en fonction de x en écrivant z= x+iy (on a y en fonction de x grâce à l'équation de la droite).On trouve : [Formule incorrecte ou erreur de parsing. Erreur 6 ] (sauf erreur de ma part)
En calculant le minimum du polynôme du dénominateur, on trouve l'abscisse du point réalisant le maximum du module de f(z), l'ordonnée est trouvée en utilisant l'équation de D.
En divisant ces coordonnées par deux, on trouve donc les coordonnées du centre présumé du cercle que l'on veut trouver. Tout ceci était en fait un travail préparatoire au brouillon (l'analyse). Ensuite, la synthèse :
On calcule le module de la différence entre f(z) et l'affixe du point que l'on vient de déterminer, et on trouve normalement une constante (indépendante de x et y) ! Ce qui permet de conclure que f(D) est bien le cercle de centre le point que l'on vient de déterminer. Ce cercle est privé de O car O ne peut effectivement pas appartenir à f(D), le module de f(z) étant toujours non nul.
Voilà, cette solution est un peu calculatoire, surtout qu'on raisonne sur une droite générale d'équation ax + by + c. Je ne parviens malheureusement pas à imaginer une solution permettant de conclure plus vite.
En ce qui concerne l'image d'un cercle de centre O :
Lorsque M parcourt ce cercle, le module de z reste constant. Donc il en est de même pour le module de f(z) (qui vaut rappelons le
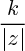 ). Donc l'image d'un cercle de centre O est un autre cercle de centre O (de rayon
). Donc l'image d'un cercle de centre O est un autre cercle de centre O (de rayon 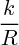 où R est le rayon du premier cercle).
où R est le rayon du premier cercle). | Documents attachés : | aucun document joint. |

