
Equations inéquations
Mathematiques > sujets expliqués - 03/11/2008 - correction
    
|
 | equations inéquations revenir au plan | docs | ||
| f(x)=({x}^{2}+x-2)({x}^2}-2x-1 lire | ||||
 | [tex]$f(x)= \left(x²+x-2\righ lire | |||
[Formule incorrecte ou erreur de parsing. Erreur 6 ] ou [Formule incorrecte ou erreur de parsing. Erreur 6 ] car un produit de facteurs est nul si et seulement si un des facteurs est nul.
Le premier des deux trinômes a un discriminant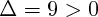 donc l'équation [Formule incorrecte ou erreur de parsing. Erreur 6 ] a deux solutions que l'on trouve à partir du discriminant en utilisant la formule vue en cours, à savoir
donc l'équation [Formule incorrecte ou erreur de parsing. Erreur 6 ] a deux solutions que l'on trouve à partir du discriminant en utilisant la formule vue en cours, à savoir 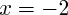 et
et 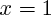 .
.
De même, le second trinôme admet deux racines (son discriminant est ) à savoir
) à savoir 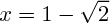 et
et 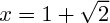
Ainsi, l'équation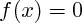 admet 4 solutions qui sont -2,
admet 4 solutions qui sont -2, 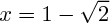 , 1 et
, 1 et 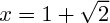 .
.
Le premier des deux trinômes a un discriminant
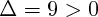 donc l'équation [Formule incorrecte ou erreur de parsing. Erreur 6 ] a deux solutions que l'on trouve à partir du discriminant en utilisant la formule vue en cours, à savoir
donc l'équation [Formule incorrecte ou erreur de parsing. Erreur 6 ] a deux solutions que l'on trouve à partir du discriminant en utilisant la formule vue en cours, à savoir 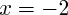 et
et 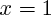 .
.De même, le second trinôme admet deux racines (son discriminant est
 ) à savoir
) à savoir 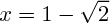 et
et 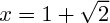
Ainsi, l'équation
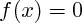 admet 4 solutions qui sont -2,
admet 4 solutions qui sont -2, 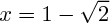 , 1 et
, 1 et 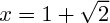 .
. | Documents attachés : | aucun document joint. |

