
Les limites
Mathematiques > sujets expliqués - 15/09/2008 - Question simple
    
|
 | Les limites revenir au plan | docs | ||
| Bien le bonjour Monsieur ou Ma lire | ||||
 | Bonjour ! Tu ne me dis pas ce lire | |||
Bonjour !
Tu ne me dis pas ce que tu as déjà trouvé !
Alors je te donne le raisonnement général pour ce genre d'exo. Je vais noter
+oo pour "plus l'infini"
+/- pour "plus ou moins"
--> pour "tend vers"
2.x pour "deux fois x".
1) Le plus simple, pour toutes les équations, c'est toujours de tracer les courbes représentatives des fonctions : ce qu'on doit trouver saute alors aux yeux. Trace donc la courbe de f et les droites D1 et D2. Vois-tu les asymptotes ? Il faut maintenant vérifier qu'on se trompe pas sur ce qu'on voit.
2) Maintenant, en regardant f(x), on tente de se faire une idée de son comportement.
*Premièrement c'est une racine carrée, donc définie uniquement pour x>0.
*Deuxièmement, sous la racine on trouve une "fraction rationnelle", en fait un rapport de deux fonctions affines toutes simples. Et les fractions ont deux types de valeurs intéressantes : celles qui annulent leur numérateur et celles qui annulent leur dénominateur. Pour les premières la fraction devient nulle (donc ici f=racine(0)=0), pour les deuxièmes la fraction vaut +/- l'infini (donc ici f(+oo)=racine(+oo)=+oo ou f=racine(-oo)=impossible). Donc si on trouve la valeur qui annule le dénominateur, f tendra vers +oo et on aura une asymptote verticale !
*Troisièmement, on va donc chercher cette valeur x1 qui donne une asymptote. Et aussi le x2 qui annule f, tant qu'on y est. Il suffit de résoudre (x1+3)=0 et (2.x2-1)=0.
*Quatrièmement : voilà, tu as une asymptote verticale en x1 !
Reste à prouver l'asymptote en +oo qu'on a vue au tout début. C'est-à-dire en fait à montrer que "très à droite" f se comporte comme une droite, c'est-à-dire encore que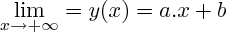 . Ici on sait même que cette fonction affine y(x) est y=b=racine(2) d'après l'énoncé. Il te reste donc à calculer cette limite en utilisant l'astuce de la factorisation par x du numérateur et du dénominateur.
. Ici on sait même que cette fonction affine y(x) est y=b=racine(2) d'après l'énoncé. Il te reste donc à calculer cette limite en utilisant l'astuce de la factorisation par x du numérateur et du dénominateur.
Rappel :
Les asymptotes à f sont des droites y=a.x+b (a ou b éventuellement nuls) telles que
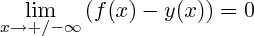
ou des fonctions x=b verticales telles que
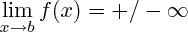
J'espère que cette fois les asymptotes n'ont plus de secret pour toi!
Grégoire CB
Tu ne me dis pas ce que tu as déjà trouvé !
Alors je te donne le raisonnement général pour ce genre d'exo. Je vais noter
+oo pour "plus l'infini"
+/- pour "plus ou moins"
--> pour "tend vers"
2.x pour "deux fois x".
1) Le plus simple, pour toutes les équations, c'est toujours de tracer les courbes représentatives des fonctions : ce qu'on doit trouver saute alors aux yeux. Trace donc la courbe de f et les droites D1 et D2. Vois-tu les asymptotes ? Il faut maintenant vérifier qu'on se trompe pas sur ce qu'on voit.
2) Maintenant, en regardant f(x), on tente de se faire une idée de son comportement.
*Premièrement c'est une racine carrée, donc définie uniquement pour x>0.
*Deuxièmement, sous la racine on trouve une "fraction rationnelle", en fait un rapport de deux fonctions affines toutes simples. Et les fractions ont deux types de valeurs intéressantes : celles qui annulent leur numérateur et celles qui annulent leur dénominateur. Pour les premières la fraction devient nulle (donc ici f=racine(0)=0), pour les deuxièmes la fraction vaut +/- l'infini (donc ici f(+oo)=racine(+oo)=+oo ou f=racine(-oo)=impossible). Donc si on trouve la valeur qui annule le dénominateur, f tendra vers +oo et on aura une asymptote verticale !
*Troisièmement, on va donc chercher cette valeur x1 qui donne une asymptote. Et aussi le x2 qui annule f, tant qu'on y est. Il suffit de résoudre (x1+3)=0 et (2.x2-1)=0.
*Quatrièmement : voilà, tu as une asymptote verticale en x1 !
Reste à prouver l'asymptote en +oo qu'on a vue au tout début. C'est-à-dire en fait à montrer que "très à droite" f se comporte comme une droite, c'est-à-dire encore que
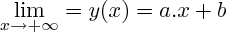 . Ici on sait même que cette fonction affine y(x) est y=b=racine(2) d'après l'énoncé. Il te reste donc à calculer cette limite en utilisant l'astuce de la factorisation par x du numérateur et du dénominateur.
. Ici on sait même que cette fonction affine y(x) est y=b=racine(2) d'après l'énoncé. Il te reste donc à calculer cette limite en utilisant l'astuce de la factorisation par x du numérateur et du dénominateur.Rappel :
Les asymptotes à f sont des droites y=a.x+b (a ou b éventuellement nuls) telles que
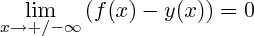
ou des fonctions x=b verticales telles que
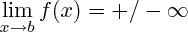
J'espère que cette fois les asymptotes n'ont plus de secret pour toi!
Grégoire CB
| Documents attachés : | aucun document joint. |

