ÉNONCÉ DE LA RELATION
Soit un système de masse m ; la dérivée de sa quantité de mouvement par rapport au temps dépend de la somme des forces qui y sont appliqués, selon la relation :
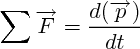
CAS PARTICULIERS
système de masse constante
comme
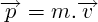
et que
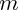
est une constante, on peut sortir
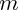
de la dérivée :
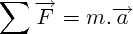
où
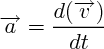
(vecteur accélération)
somme des forces nulle :
lorsque la somme des forces appliquées au système est nulle
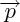
est constant
Si de plus le système est
de masse constante,
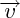
est constant : on retrouve le
principe d'inertie (programme de 1
ère S), qui n'est donc qu'un cas particulier de la relation fondamentale de la dynamique.
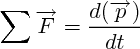
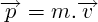 et que
et que 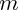 est une constante, on peut sortir
est une constante, on peut sortir 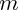 de la dérivée :
de la dérivée :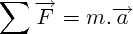
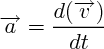 (vecteur accélération)
(vecteur accélération)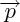 est constant
est constant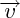 est constant : on retrouve le principe d'inertie (programme de 1ère S), qui n'est donc qu'un cas particulier de la relation fondamentale de la dynamique.
est constant : on retrouve le principe d'inertie (programme de 1ère S), qui n'est donc qu'un cas particulier de la relation fondamentale de la dynamique.