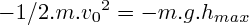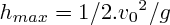THÉORÈME
la variation d'énergie cinétique d'un système sur un trajet, est égale à la somme des travaux des forces appliquées au système, sur ce trajet.
Exemple
On lance un objet vers le haut : si on néglige les frottements, la seule force qui s'applique à l'objet est son poids : comme le trajet est ascendant, le poids a un travail négatif : l'énergie cinétique de l'objet diminue (il ralentit, en montant) ; si on tient compte des frottements (qui s'opposent au mouvement) : leur travail s'ajoute à celui du poids, ce qui fait que l'énergie cinétique diminue en réalité plus rapidement que ce qu'on trouve en négligeant les frottements.
CONSIDÉRATIONS ÉNERGÉTIQUES
Soit un système qui se déplace sans frottements : son
énergie mécanique (rappel : c'est la somme :
énergie cinétique +
énergies potentielles) est constante. Donc :
- les
variations d'énergie cinétique, et
de la somme des énergies potentielles, sont égales en valeur absolue, et de signes opposés ; le théorème de l'énergie cinétique implique donc que la somme des travaux des forces appliquées au système est égale à la somme des variations d'énergies potentielles :
- le
travail du poids est égal aux variations d'énergie potentielle de pesanteur ;
- le
travail de la force de Coulomb est égal aux variations d'énergie potentielle de Coulomb, donc la somme des travaux des forces est égale à la somme des variations d'énergies potentielles.
Si le système est soumis aux frottements : son énergie mécanique diminue, donc les variations d'énergie potentielle et d'énergie cinétique ne sont plus opposées.
Exemple d'application
On lance une masse 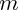 vers le haut, avec une vitesse initiale
vers le haut, avec une vitesse initiale 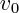 ; calculer la hauteur maximale qu'elle atteindra, en négligeant les frottements.
; calculer la hauteur maximale qu'elle atteindra, en négligeant les frottements.
Pendant l'ascension (depuis le lancement, jusqu'au point de hauteur maximale, où la vitesse de la masse s'annulera), la seule force qui s'applique au système est son poids ; d'après le théorème de l'énergie cinétique appliqué entre le lancement, et le point de hauteur maximale, nous avons donc :
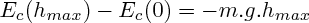
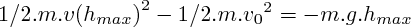
Or 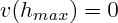 , donc
, donc
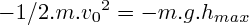
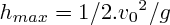
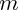 vers le haut, avec une vitesse initiale
vers le haut, avec une vitesse initiale 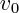 ; calculer la hauteur maximale qu'elle atteindra, en négligeant les frottements.
; calculer la hauteur maximale qu'elle atteindra, en négligeant les frottements.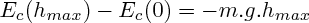
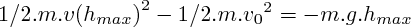
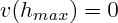 , donc
, donc